
 如图所示,斜面直轨道是粗糙的,大、小圆轨道光滑且均与斜面直轨道相切,其中小圆轨道半径为R,切点分别为C、B,圆形轨道的出入口错开,大、小圆轨道的最高点跟斜面的最高点在同一水平线上,斜面直轨道的倾角为60°.今有一质量为m的小球自A以初速度v0沿斜面滑下,运动到B后进入小圆形轨道,接着再沿斜面下滑进入大圆形轨道运动,小球与斜面间的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,求:
如图所示,斜面直轨道是粗糙的,大、小圆轨道光滑且均与斜面直轨道相切,其中小圆轨道半径为R,切点分别为C、B,圆形轨道的出入口错开,大、小圆轨道的最高点跟斜面的最高点在同一水平线上,斜面直轨道的倾角为60°.今有一质量为m的小球自A以初速度v0沿斜面滑下,运动到B后进入小圆形轨道,接着再沿斜面下滑进入大圆形轨道运动,小球与斜面间的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,求:分析 (1)根据几何关系求出大圆的半径,根据牛顿第二定律求出最高点的临界速度,通过动能定理求出初速度应满足的条件.
(2)根据动能定理求出小球在小圆轨道最高点的速度,从而根据牛顿第二定律求出弹力的大小.
解答 解:(1)设C处圆形轨道的半径为R′,则由几何关系可知,A到B处圆轨圆心的距离为:
AO1=$\frac{R}{sin30°}$=2R,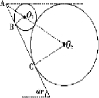
而且 $\frac{R′}{3R+R′}$=sin30°,
解得:R′=3R,
斜面轨道AB=Rcot30°=$\sqrt{3}$R=S1…①
AC=3Rcot30°=3$\sqrt{3}$R=S2…②
小球由A到C处圆形轨道的最高点的过程由动能定理有:
-μmgcos60°•S2=$\frac{1}{2}$mv2-$\frac{1}{2}$mv02…③
由于小球恰能到达C处圆轨道的最高点,故v=$\sqrt{gR′}$=$\sqrt{3gR}$…④
联立①②③④解得:v0=$\sqrt{\frac{9}{2}gR}$…⑤
(2)设小球到达B处圆形轨道的最高点的速度为v1,
小球由A到B处圆形轨道最高点的过程,由动能定理有:
-μmgcos60°•S1=$\frac{1}{2}$mv12-$\frac{1}{2}$mv02…⑥
设小球在B处圆形轨道最高点受轨道压力为FN,
由牛顿第二定律可知,FN+mg=m$\frac{{v}_{1}^{2}}{R}$…⑦
联立①⑤⑥⑦解得:FN=3mg.
答:(1)小球恰能到达大圆轨道的最高点,则v0应满足大于或等于$\sqrt{\frac{9}{2}gR}$;
(2)小球在小圆轨道的最高点时受到的轨道的弹力大小是3mg.
点评 本题考查了圆周运动和动能定理、牛顿第二定律的综合,知道圆周运动向心力的来源是解决本题的关键,本题对数学几何能力的要求较高,需加强训练.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:多选题
| A. | 当分子间作用力表现为斥力时,分子势能随分子间距离的增大而增大 | |
| B. | 温度高的物体分子平均动能一定大,内能也一定大 | |
| C. | 昆虫可以停在水面上,主要是液体表面张力的作用 | |
| D. | 热力学第二定律指出:在任何自然的过程中,一个孤立的系统的总熵不会减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,质量为M=60kg的人和m=40kg箱子,一起以v0=10m/s的速度在光滑水平的冰面上匀速滑行,前进中突然发现前方有一矮墙.为避免撞墙,人将质量m=40kg的箱子水平推向墙,箱子撞墙后以原速率反向弹回,之后人又接住箱子.求人推出箱子的速度至少多大才能在完成一次推接后避免撞墙墙.
如图,质量为M=60kg的人和m=40kg箱子,一起以v0=10m/s的速度在光滑水平的冰面上匀速滑行,前进中突然发现前方有一矮墙.为避免撞墙,人将质量m=40kg的箱子水平推向墙,箱子撞墙后以原速率反向弹回,之后人又接住箱子.求人推出箱子的速度至少多大才能在完成一次推接后避免撞墙墙.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
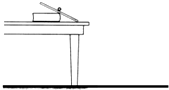 如图所示,在水平桌面上用练习本做成一个斜面,使小钢球从斜面上某一位置滚下,钢球沿桌面飞出后做平抛运动.利用此装置来测量小钢球离开桌面的初速度,请你完成以下研究方案.
如图所示,在水平桌面上用练习本做成一个斜面,使小钢球从斜面上某一位置滚下,钢球沿桌面飞出后做平抛运动.利用此装置来测量小钢球离开桌面的初速度,请你完成以下研究方案.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一个质量为m=2kg的物体,受到与水平方向成37°角斜向右下方的推力F1=10N的作用,在水平面上运动了S1=2m后撤去推力,物体又滑行S2=1.6m后静止,若物体与水平面间的滑动摩擦力为它们之间弹力的0.2倍,求:
如图所示,一个质量为m=2kg的物体,受到与水平方向成37°角斜向右下方的推力F1=10N的作用,在水平面上运动了S1=2m后撤去推力,物体又滑行S2=1.6m后静止,若物体与水平面间的滑动摩擦力为它们之间弹力的0.2倍,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
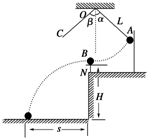 用如图所示装置来进行探究碰撞的不变量的实验,质量为mB的钢球B放在小支柱N上,球心离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,且细线与竖直线之间夹角为α.球A由静止释放,摆到最低点时恰与球B发生正碰,碰撞后,A球把轻质指示针C推移到与竖直线夹角为β处,B球落到地面上,地面上铺有一张覆盖有复写纸的白纸D,用来记录球B的落点.保持α角度不变,多次重复上述实验,在白纸上记录到多个B球的落地点.
用如图所示装置来进行探究碰撞的不变量的实验,质量为mB的钢球B放在小支柱N上,球心离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,且细线与竖直线之间夹角为α.球A由静止释放,摆到最低点时恰与球B发生正碰,碰撞后,A球把轻质指示针C推移到与竖直线夹角为β处,B球落到地面上,地面上铺有一张覆盖有复写纸的白纸D,用来记录球B的落点.保持α角度不变,多次重复上述实验,在白纸上记录到多个B球的落地点.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,将a、b两小球以大小均为10$\sqrt{6}$m/s的初速度分别从A、B两点相差1s先后水平相向抛出(A点比B点高),a小球从A点抛出后,经过时间t,a、b两小球恰好在空中相遇,此时速度方向相互垂直,不计空气阻力,取g=10m/s2.则从a小球抛出到两小球相遇,小球a下落的时间t和高度h分别是( )
如图所示,将a、b两小球以大小均为10$\sqrt{6}$m/s的初速度分别从A、B两点相差1s先后水平相向抛出(A点比B点高),a小球从A点抛出后,经过时间t,a、b两小球恰好在空中相遇,此时速度方向相互垂直,不计空气阻力,取g=10m/s2.则从a小球抛出到两小球相遇,小球a下落的时间t和高度h分别是( )| A. | t=2s | B. | t=3s | C. | h=45 m | D. | h=20m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com