
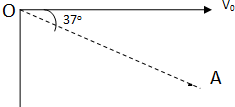
 滑雪运动可抽象为物体在斜坡上的平抛运动.如图所示,设可视为质点的滑雪运动员,从斜坡顶端O处,以初速度v0水平滑出,在运动过程中恰好通过P点,OP与水平方向夹角为37°,则滑雪运动员到达P点时的动能与滑出时的动能比值为(不计空气阻力,sin37°=0.6,cos37°=0.8)( )
滑雪运动可抽象为物体在斜坡上的平抛运动.如图所示,设可视为质点的滑雪运动员,从斜坡顶端O处,以初速度v0水平滑出,在运动过程中恰好通过P点,OP与水平方向夹角为37°,则滑雪运动员到达P点时的动能与滑出时的动能比值为(不计空气阻力,sin37°=0.6,cos37°=0.8)( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{13}{4}$ | D. | $\frac{4}{13}$ |
分析 运动员做平抛运动,到达P点时竖直位移与水平位移之比等于tan37°,结合分位移公式求出时间,再由速度的合成求出到达P点的速度,即可求解动能的关系.
解答 解:由图知 tan37°=$\frac{y}{x}$=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}$=$\frac{gt}{2{v}_{0}}$,
解得:t=$\frac{2{v}_{0}tan37°}{g}$
滑雪运动员在P点时竖直速度 vy=gt=$\frac{3}{2}{v}_{0}$
滑雪运动员到达P点的动能 EkA=$\frac{1}{2}m{v}_{0}^{2}+\frac{1}{2}m{v}_{y}^{2}$=$\frac{13}{8}m{v}_{0}^{2}$,
滑出时的动能 Ek0=$\frac{1}{2}m{v}_{0}^{2}$,
所以滑雪运动员到达P点时的动能与滑出时的动能比值为$\frac{13}{4}$.故C正确.
故选:C
点评 本题考查平抛运动规律的应用,关键要能够灵活利用分位移公式求得t和的表达式,要注意斜坡的倾角反映位移与水平方向的夹角,而不是速度与水平方向的夹角.


科目:高中物理 来源: 题型:多选题
| A. | E=$\frac{F}{q}$是电场中某点的电场强度的定义式,是用比值法定义的物理量,场强由电场本身决定,与F和q无关 | |
| B. | 由φ=$\frac{{E}_{P}}{q}$可知,电场中某点的电势φ与q成反比 | |
| C. | 由Uab=E•d可知匀强电场中任意两点a、b间距离越大,则两点间电势差也一定越大 | |
| D. | E=$\frac{kQ}{{r}^{2}}$是真空中点电荷场强的计算式,E与Q成正比,与r的平方成反比,其中Q为场源电荷 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 放射性元素与别的元素形成化合物时仍具有放射性 | |
| B. | 一个原子核在一次衰变中的氢原子可同时放出α、β和γ三种射线 | |
| C. | 一个处于n=4的激发态的氢原子向低能级跃迁时,可能产生上的谱线最多为3条 | |
| D. | ${\;}_{90}^{232}$Th变为${\;}_{82}^{208}$Pb要经过6次α衰变和4次β衰变 | |
| E. | α、β和γ三种射线中,α射线的穿透能力最强 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 牛顿在得出力不是维持物体运动的原因这一结论的过程中运用了理想实验的方法 | |
| B. | 在“探究弹性势能的表达式”的活动中,为计算弹簧弹力所做功,把拉伸弹簧的过程分为很多小段,拉力在没小段可以认为是恒力,用各小段做功的代数和代表弹力的整个过程所做的功,物理学中把这种研究方法叫做“微元法”,那么由加速度的定义a=$\frac{△v}{△t}$,当△t非常小的时候,$\frac{△v}{△t}$就可以表示物体在t时刻的瞬时加速度,上述论断就运用了“微元法” | |
| C. | 用比值法定义物理量是物理学中一种重要的物理科学方法,公式a=$\frac{F}{m}$就运用了比值定义法 | |
| D. | 万有引力可以理解为任何有质量的物体都要在其周围空间产生一个引力场,而一个有质量的物体在其它有质量的物体所产生的引力场中都要受到该引力场的引力(即万有引力)作用,这情况可以与电场相类比,那么在地球的引力场中的重力加速度就可以与电场中的电场强度相类比 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
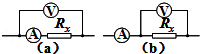 伏安法是一种常用的测量导体电阻的方法,某同学分别用如图(a)、(b)两种接法测量一个电阻器的阻值,以下结论正确的是( )
伏安法是一种常用的测量导体电阻的方法,某同学分别用如图(a)、(b)两种接法测量一个电阻器的阻值,以下结论正确的是( )| A. | 用图(a)接法测得的电阻值偏大 | |
| B. | 用图中两种接法测得的电阻值都偏小 | |
| C. | 用图(b)接法测得的电阻值偏大 | |
| D. | 用图中两种接法测得的电阻值都偏大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 两灯的电阻之比RA:RB=4:1 | |
| B. | 在相同时间内,两灯实际发热之比QA:QB=1:2 | |
| C. | 两灯的实际电压之比UA:UB=2:1 | |
| D. | 两灯实际消耗的功率之比PA:PB=1:2 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 速度变化方向为正,加速度方向为负 | |
| B. | 速度变化越来越快,加速度越来越小 | |
| C. | 匀变速直线运动是速度变化量恒定的运动 | |
| D. | 速度为正,加速度可能为负 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com