
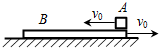
 如图所示,一质量为M、长为L的长方形木板B放在光滑的水平地面上,在其右端放一质量为m的小木块A,m<M.现以地面为参照系,给A和B以大小相等、方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A刚好没有滑离B板,以地面为参照系.
如图所示,一质量为M、长为L的长方形木板B放在光滑的水平地面上,在其右端放一质量为m的小木块A,m<M.现以地面为参照系,给A和B以大小相等、方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A刚好没有滑离B板,以地面为参照系.分析 (1)系统置于光滑水平面,其所受合外力为零,系统总动量守恒,A最后刚好没有滑离B板,两者的速度相同,根据动量守恒定律即可求解;产生的热量等于初末系统总动能之差.
(2)恰好没有滑离,根据动能定理求出相对滑动产生的热量,向左运动到达最远处时速度为0,由动能定理列式,联立方程即可求解.
解答 解:(1)A刚好没有滑离B板时,vA=vB=v,A在B的最左端,设向右为正方向,则有:
Mv0-mv0=(M+m)v
解得:$v=\frac{M-m}{M+m}{v}_{0}$,
因m<M,则V>0,说明共同速度方向向右.
产生的热量等于A、B系统损失的机械能:$Q=\left.\begin{array}{l}{△E=\frac{1}{2}m{V}_{0}^{2}+\frac{1}{2}M{V}_{0}^{2}-\frac{1}{2}(M+m){V}^{2}}\end{array}\right.$=$\frac{2Mm{v}_{0}^{2}}{M+m}$
(2)当小木块A向左运动到达的最远处时,A向左减速为零时,设向右为正方向,则有:
Mv0-mv0=MvB+0
得:${v}_{B}=\frac{M-m}{M}{v}_{0}$
(3)由于最后A刚好没有滑离B板,A、B系统损失的机械能转化为热能:
$μmgL=\frac{2Mm{v}_{0}^{2}}{M+m}$
由上式得:$μ=\frac{2M{v}_{0}^{2}}{(M+m)gL}$
当B的速度减小到vB的过程中,由动能定理得:$-μmg{S}_{B}=\frac{1}{2}M{v}_{B}^{2}-\frac{1}{2}M{v}_{0}^{2}$
所以:SB=$\frac{(2Mm-{m}^{2})(M+m)}{4{M}^{2}m}•L$
答:(1)若已知A和B的初速度大小为v0,它们最后的速度$\frac{M-m}{M+m}{v}_{0}$,方向向右;所产生的热量Q是$\frac{2Mm{v}_{0}^{2}}{M+m}$.
(2)若已知A和B的初速度大小为v0,当小木块A向左运动到达的最远处时(从地面上看),B的速度vB是$\frac{M-m}{M}{v}_{0}$;
(3)若初速度的大小未知,当小木块A向左运动到达的最远处时(从地面上看),B所发生的位移是$\frac{(2Mm-{m}^{2})(M+m)}{4{M}^{2}m}•L$.
点评 本题关键要判断出系统的动量守恒,准确把握临界条件,并结合动能定理求解.


 培优三好生系列答案
培优三好生系列答案科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,轻弹簧的左端固定在墙上,右端固定在放于粗糙水平面的物块M上,当物块处在O处时弹簧处于自然状态,现将物块拉至P点后释放,则物块从P点返回O处的过程中( )
如图所示,轻弹簧的左端固定在墙上,右端固定在放于粗糙水平面的物块M上,当物块处在O处时弹簧处于自然状态,现将物块拉至P点后释放,则物块从P点返回O处的过程中( )| A. | 物块的速度不断增大,而加速度不断减小 | |
| B. | 物块的速度先增后减,而加速度先减后增 | |
| C. | 物块的速度不断减小,而加速度不断增大 | |
| D. | 物块的速度先增后减,而加速度不断减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某同学把附有滑轮的长木板放在实验桌上,将细绳一端拴在小车上,另一端绕过定滑轮,挂上适当的钩码,使小车在钩码的牵引下运动,以此定量探究绳拉力做功与小车速度变化的关系,此外还准备了打点计时器及配套的电源、导线、复写纸、纸带、小木块等.组装的实验装置如图所示.
某同学把附有滑轮的长木板放在实验桌上,将细绳一端拴在小车上,另一端绕过定滑轮,挂上适当的钩码,使小车在钩码的牵引下运动,以此定量探究绳拉力做功与小车速度变化的关系,此外还准备了打点计时器及配套的电源、导线、复写纸、纸带、小木块等.组装的实验装置如图所示.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 该卫星在轨道上的运行速度大于第一宇宙速度 | |
| B. | 该卫星在轨道上运行一周需要的时间就是地球自转一周的时间 | |
| C. | 该卫星内的仪器处于失重状态,所受地球引力等于零 | |
| D. | 该卫星离地面的距离可能是地球半径的2倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,甲从高H处以初速度v1水平抛出小球A,乙同时从地面以初速度v2竖直上抛小球B,在B尚未到达最高点之前,两球在空中相遇,则( )
如图所示,甲从高H处以初速度v1水平抛出小球A,乙同时从地面以初速度v2竖直上抛小球B,在B尚未到达最高点之前,两球在空中相遇,则( )| A. | 从抛出到两球相遇所用时间为t=$\frac{H}{v_1}$ | |
| B. | 抛出前两球的水平距离s=$\frac{{H{v_1}}}{v_2}$ | |
| C. | 相遇时A球速率vA=$\frac{gH}{v_2}$ | |
| D. | 若v2=$\sqrt{gH}$,则两球相遇在$\frac{H}{2}$处 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com