
| A�� | �����ǵĵ�һ�����ٶ�Ϊ$\frac{��R}{T}$ | |
| B�� | ����ɴ��Ƹ�������Բ���˶������ڲ�С�ڦ�t$\sqrt{\frac{2R}{h}}$ | |
| C�� | �����ǵ�ƽ���ܶ�Ϊ$\frac{3h}{2G��{t}^{2}}$ | |
| D�� | ��������Ǵ���һ��ͬ�����ǣ�������DZ���߶�Ϊ$\root{3}{\frac{h{T}^{2}{R}^{2}}{2{��}^{2}{t}^{2}}}$ |
���� �������������˶�������������������ٶȣ��ٸ������������ṩԲ���˶����������ۼ��ɣ�
��� �⣺�������������˶�������������������ٶ�$g=\frac{2h}{{t}^{2}}$
A������ĵ�һ�����ٶ�$v=\sqrt{gR}=\sqrt{\frac{2h}{{t}^{2}}R}$����A����
B���������������ṩԲ���˶��������У�$G\frac{mM}{{r}^{2}}=mr\frac{4{��}^{2}}{{T}^{2}}$�ɵ����ǵ�����T=$\sqrt{\frac{4{��}^{2}{r}^{3}}{GM}}$����֪����뾶ԽС����ԽС�����ǵ���С�뾶ΪR����������СֵΪ${T}_{min}=\sqrt{\frac{4{��}^{2}{R}^{3}}{GM}}=\sqrt{\frac{4{��}^{2}{R}^{3}}{g{R}^{2}}}=\sqrt{\frac{4{��}^{2}R}{\frac{2h}{{t}^{2}}}}$=$��t\sqrt{\frac{2R}{h}}$����B��ȷ��
C����$G\frac{mM}{{R}^{2}}=mg=m\frac{2h}{{t}^{2}}$�У�M=$\frac{2h{R}^{2}}{G{t}^{2}}$������������ܶ�$��=\frac{M}{V}=\frac{\frac{2h{R}^{2}}{G{t}^{2}}}{\frac{4}{3}��{R}^{3}}=\frac{3h}{2G{t}^{2}R��}$����C����
D��ͬ�����ǵ�������������ת������ͬ���У�$G\frac{mM}{��R+h��^{2}}=m��R+h��\frac{4{��}^{2}}{{T}^{2}}$���������ݽ�ã�h=$\root{3}{\frac{h{T}^{2}{R}^{2}}{2{��}^{2}{t}^{2}}}$-R����D����
��ѡ��B��
���� ����ؼ���ͨ�����������˶�������������������ٶȣ��ٸ������������ṩԲ���˶���������������������������⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
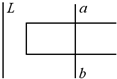 ��ͼ��ʾ��ͨ��ֱ����L��ƽ�е�����ͬһƽ���ڣ�������ab��ֹ�ڵ����ϲ��뵼����ɱպϻ�·��ab���ص������ɻ�������ͨ�絼��L�����˶�ʱ��������
��ͼ��ʾ��ͨ��ֱ����L��ƽ�е�����ͬһƽ���ڣ�������ab��ֹ�ڵ����ϲ��뵼����ɱպϻ�·��ab���ص������ɻ�������ͨ�絼��L�����˶�ʱ��������| A�� | ab�������� | |
| B�� | ab�������һ��� | |
| C�� | ab���Ա��־�ֹ | |
| D�� | ab�����˶�������ͨ�絼���ϵ��������й� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ�����һͷP�ù⻬��̶�����ֱǽ���ϣ��˿���P��ת��������һͷO������������ǽ��A�㣬һ���屻������O�㣬��ǡ��ˮƽ�����ڽ�ǽ���������ҵ����ƣ�ͬʱ�ӳ�����ʹ���Ա���ˮƽ������������ѹ��������������������˵����ȷ���ǣ�������
��ͼ��ʾ�����һͷP�ù⻬��̶�����ֱǽ���ϣ��˿���P��ת��������һͷO������������ǽ��A�㣬һ���屻������O�㣬��ǡ��ˮƽ�����ڽ�ǽ���������ҵ����ƣ�ͬʱ�ӳ�����ʹ���Ա���ˮƽ������������ѹ��������������������˵����ȷ���ǣ�������| A�� | ���߾���С | B�� | ���߾����� | ||
| C�� | �����ѹ������������������С | D�� | �����ѹ����С���������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
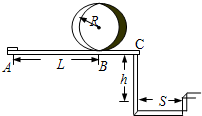 ijУ������ȤС���������ң����������������·����ͼ��ʾ�����������A��������ˮƽֱ�߹���˶�L����B�����뾶ΪR�Ĺ⻬��ֱԲ������뿪��ֱԲ���������ڹ⻬ƽֱ������˶���C�㣬����Խ����������֪��������m=0.1kg��ͨ����Զ����P=1.5W������������ֱԲ���ǰ�ܵ���������Ϊ0.3N��������˶����ܵ����������ɲ��ƣ�ͼ��L=10.00m��R=0.32m��h=1.25m��S=1.50m��
ijУ������ȤС���������ң����������������·����ͼ��ʾ�����������A��������ˮƽֱ�߹���˶�L����B�����뾶ΪR�Ĺ⻬��ֱԲ������뿪��ֱԲ���������ڹ⻬ƽֱ������˶���C�㣬����Խ����������֪��������m=0.1kg��ͨ����Զ����P=1.5W������������ֱԲ���ǰ�ܵ���������Ϊ0.3N��������˶����ܵ����������ɲ��ƣ�ͼ��L=10.00m��R=0.32m��h=1.25m��S=1.50m���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
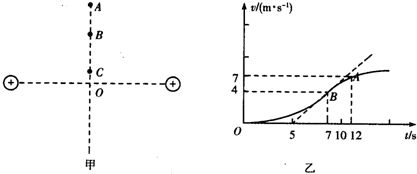
| A�� | ��C�㵽A�㣬�������� | |
| B�� | B��A�����ĵ��Ʋ�ΪUBA=8.25V | |
| C�� | ��C�㵽A�����ĵ������ȼ�С���� | |
| D�� | B��Ϊ�д����ϵ糡ǿ�����ĵ㣬��ǿE=1V/m |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��˹�ط����˵����Ĵ�ЧӦ���������о���������ϵ����ϵ | |
| B�� | �����ڷ����˵�Ÿ�Ӧ����һ�������˵���������������ϵ | |
| C�� | ���ط����˵�����ЧӦ�Ĺ��ɣ����Եظ����˵��ܺ�����֮���ת����ϵ | |
| D�� | ����������˳��ĸ�����õ糡�ߺʹŸ�������������糡�ʹų� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ��������� m��=$\frac{{g{R^2}}}{G}$ | |
| B�� | ̫��������m̫=$\frac{{4{��^2}L_2^3}}{GT_2^2}$ | |
| C�� | ���������m��=$\frac{{4{��^2}L_1^3}}{GT_1^2}$ | |
| D�� | �������������M��֪������������̫�����ܶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
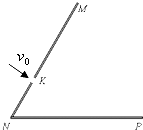 ��ͼ��ʾ����б����NM�ϵ�һ��С��K��NM��ˮƽ����NP��60��ǣ�K��N��ľ���$\overline{KN}$=a����������Ϊm�������Ϊq������������ɵ�����������ֱ����б����NM�����ٶ�v0�������룬�����������ܵ�������
��ͼ��ʾ����б����NM�ϵ�һ��С��K��NM��ˮƽ����NP��60��ǣ�K��N��ľ���$\overline{KN}$=a����������Ϊm�������Ϊq������������ɵ�����������ֱ����б����NM�����ٶ�v0�������룬�����������ܵ��������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com