
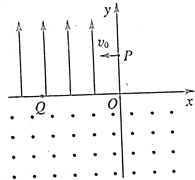
 如图所示,在xOy平面内,第二象限中有匀强电场,方向沿y轴正方向,在第四象限有匀强磁场,方向垂直于xOy平面问外.今有一个质量为m,电量为e的电子(不计重力),从y轴上的P(0,L)点以垂直于y轴、大小为v0的初速度射入电场,经电场偏转后从x轴上的Q(-2L,0)点进入磁场,并能返回到出发点P.求:
如图所示,在xOy平面内,第二象限中有匀强电场,方向沿y轴正方向,在第四象限有匀强磁场,方向垂直于xOy平面问外.今有一个质量为m,电量为e的电子(不计重力),从y轴上的P(0,L)点以垂直于y轴、大小为v0的初速度射入电场,经电场偏转后从x轴上的Q(-2L,0)点进入磁场,并能返回到出发点P.求:分析 (1)电子在电场做做类平抛运动,应用类平抛运动规律与动能定理求出h;
(2)电子在磁场中做匀速圆周运动,应用牛顿第二定律可以求出B;
(3)求出电子在电场、磁场、第二象限中的运动时间,然后求出电子总的运动时间.
解答 解:(1)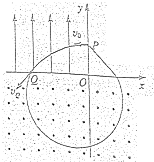 电子射入电场后做类平抛运动,竖直方向有:
电子射入电场后做类平抛运动,竖直方向有:
L=$\frac{1}{2}•\frac{eE}{m}{t}^{2}$
水平方向有:
2L=v0t
联立解得:E=$\frac{m{v}_{0}^{2}}{2eL}$
(2)电子进入磁场时的竖直分速度为:vy=$\frac{eE}{m}t$=v0;
所以进入磁场时的合速度为:vQ=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{2}{v}_{0}$,方向与x轴负方向成45°角(如图).
电子离开磁场后沿直线运动经P点,所以其轨迹如图所示,由几何知识知,电子在磁场中做圆周运动的半径为:r=$\frac{3\sqrt{2}}{2}L$
由evQB=m$\frac{{v}_{Q}^{2}}{r}$
可得 B=$\frac{2m{v}_{0}}{3eL}$
(3)当电子以速度vQ′进入磁场时速度与x轴负向间的夹角设为θ,则
vQ′=$\frac{{v}_{y}}{sinθ}$=$\frac{{v}_{0}}{sinθ}$
电子运动半径为r′,则有 evQ′B=m$\frac{v{′}_{Q}^{2}}{r}$
射入点与射出点的距离 d=2r′•sinθ
由以上各式得:d=3L
可见射入磁场的点和射出磁场的点之间的距离 d与初速度大小无关,所以要使电子经过O点,射入磁场的点距O点的距离应为 d=3L,故其初速度应为
v′0=$\frac{3L}{t}$=3L$•\frac{{v}_{0}}{2L}$=$\frac{3}{2}{v}_{0}$
答:(1)电场强度的大小是$\frac{m{v}_{0}^{2}}{2eL}$;
(2)磁感应强度的大小是$\frac{2m{v}_{0}}{3eL}$;
(3)电子仍从P点垂直于y轴射入电场时的初速度应为$\frac{3}{2}{v}_{0}$.
点评 电子在电场中做类平抛运动的研究方法是运动的分解,而磁场中圆周运动的研究方法是画轨迹,都常用的思路.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中物理 来源: 题型:选择题
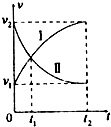 从同一地点同时开始沿同一直线运动的两个物体I、II的速度图象如图所示,在0~t2时间内,下列说法中正确的是( )
从同一地点同时开始沿同一直线运动的两个物体I、II的速度图象如图所示,在0~t2时间内,下列说法中正确的是( )| A. | Ⅰ、Ⅱ两个物体在t1时刻相遇 | |
| B. | Ⅰ、Ⅱ两个物体的平均速度大小都是$\frac{{{v_1}+{v_2}}}{2}$ | |
| C. | Ⅰ、Ⅱ两个物体所受的合外力都在不断减小 | |
| D. | Ⅰ物体的加速度不断增大,Ⅱ物体的加速度不断减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 伽利略在亚里士多德、笛卡尔等科学家关于力与运动关系研究的基础上,运用理想实验和归谬法得出了惯性定律 | |
| B. | 法拉第首先提出了场的概念,并用电场线和磁感线形象地描述电场和磁场 | |
| C. | 卡文迪许巧妙地运用扭秤实验,成功测出了静电力常量的数值 | |
| D. | 牛顿接受了胡克等科学家关于“吸引力与两中心距离的平方成反比”的猜想,运用严密的逻辑推理,建立了万有引力定律 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
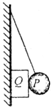 如图所 示用轻绳将光滑小球P悬挂于竖直墙壁上,在墙壁和小球P之间夹着矩形物块Q,P、Q均处于静止状态,则下列说法正确的是( )
如图所 示用轻绳将光滑小球P悬挂于竖直墙壁上,在墙壁和小球P之间夹着矩形物块Q,P、Q均处于静止状态,则下列说法正确的是( )| A. | 物块Q受到3个力 | |
| B. | 物体P受4个力 | |
| C. | 若绳子变长,则绳子的拉力将变小 | |
| D. | 若绳子变短,则Q受到的静摩擦力将增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一定质量的理想气体按p-T图象中箭头方向,从状态A变化到状态B,再变化到状态C,已知气体在状态A时的体积为33.6L.
如图所示,一定质量的理想气体按p-T图象中箭头方向,从状态A变化到状态B,再变化到状态C,已知气体在状态A时的体积为33.6L.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
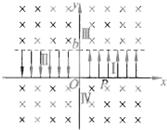 如图所示,在平面直角坐标系xoy中,在O≤y≤b且x>0的区域I内分布着沿y轴正方向的匀强电场,电场强度为E;在0≤y≤b且x<0的区域II内分布着沿y轴负方向的匀强电场,电场强度也为E;在y>b的区域Ⅲ和y<0的区域IV内存在垂直于纸面向里、大小可调节的匀强磁场.质量为m,电荷量为+q的粒子由P(b,0)点静止释放,经电场加速和磁场偏转后又回到P点.已知粒子在磁场区域Ⅲ和Ⅳ中始终做轨道半径为b的匀速圆周运动.粒子重力不计且不考虑磁场变化所引起的电场效应.
如图所示,在平面直角坐标系xoy中,在O≤y≤b且x>0的区域I内分布着沿y轴正方向的匀强电场,电场强度为E;在0≤y≤b且x<0的区域II内分布着沿y轴负方向的匀强电场,电场强度也为E;在y>b的区域Ⅲ和y<0的区域IV内存在垂直于纸面向里、大小可调节的匀强磁场.质量为m,电荷量为+q的粒子由P(b,0)点静止释放,经电场加速和磁场偏转后又回到P点.已知粒子在磁场区域Ⅲ和Ⅳ中始终做轨道半径为b的匀速圆周运动.粒子重力不计且不考虑磁场变化所引起的电场效应.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示边长为L的正方形内有磁感应强度为B的匀强磁场,在A、B、C、D、E五点处都开有小孔,不同速度的电子从A孔入射后,在B、C、D都有电子射出.图中α=30°,则求:
如图所示边长为L的正方形内有磁感应强度为B的匀强磁场,在A、B、C、D、E五点处都开有小孔,不同速度的电子从A孔入射后,在B、C、D都有电子射出.图中α=30°,则求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | vm可为许多值,与al、a2的大小有关 | B. | vm可为许多值,与a1、a2的大小无关 | ||
| C. | a1、a2必须满足$\frac{{a}_{1}{a}_{2}}{{a}_{1}+{a}_{2}}$=$\frac{2v}{t}$ | D. | a1、a2必须是一定的 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com