
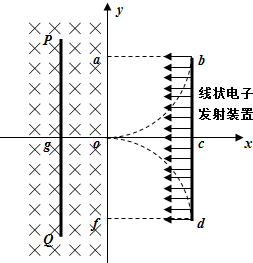
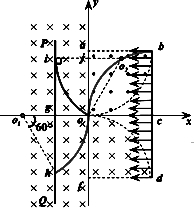
 如图所示,直角坐标系的y轴左方为垂直纸面向里的匀强磁场,磁感应强度的大小为B;垂直x轴竖直放置一个足够大接收屏PQ,它离原点距离为og=L/2;直角坐标系的第一象限和第四象限的abco、ocdf均是边长为L的正方形,内各有一垂直纸面方向的半径为L的1/4圆形匀强磁场区域;磁感应强度的大小均为B.bd为一线状发射装置,射出一束质量为m、电荷量为e的电子,以相同的初速度沿纸面垂直于bd边射入两个正方形区域,电子从bd边上的任意点入射,都只能从原点O射出进入y轴左方磁场.(不考虑电子之间的相互作用,不计重力)求:
如图所示,直角坐标系的y轴左方为垂直纸面向里的匀强磁场,磁感应强度的大小为B;垂直x轴竖直放置一个足够大接收屏PQ,它离原点距离为og=L/2;直角坐标系的第一象限和第四象限的abco、ocdf均是边长为L的正方形,内各有一垂直纸面方向的半径为L的1/4圆形匀强磁场区域;磁感应强度的大小均为B.bd为一线状发射装置,射出一束质量为m、电荷量为e的电子,以相同的初速度沿纸面垂直于bd边射入两个正方形区域,电子从bd边上的任意点入射,都只能从原点O射出进入y轴左方磁场.(不考虑电子之间的相互作用,不计重力)求:
| ||
| r |
| eBL |
| m |
| L |
| 2 |
| L |
| 2 |
| r2-x2 |
| ||
| 2 |
| L |
| 2 |
| L |
| 2 |
r2
|
| ||
| 2 |
| 1 |
| 4 |
| T |
| 4 |
| 1 |
| 4 |
| 2πm |
| eB |
| πm |
| 2eB |
| T |
| 6 |
| 1 |
| 6 |
| 2πm |
| eB |
| πm |
| 3eB |
| 5πm |
| 6eB |
| eBL |
| m |
| ||
| 2 |
| ||
| 2 |
| 5πm |
| 6eB |


 综合自测系列答案
综合自测系列答案科目:高中物理 来源: 题型:
 (2009?宁夏)空间有一均匀强电场,在电场中建立如图所示的直角坐标系O-xyz,M、N、P为电场中的三个点,M点的坐标(0,a,0),N点的坐标为(a,0,0),P点的坐标为(a,
(2009?宁夏)空间有一均匀强电场,在电场中建立如图所示的直角坐标系O-xyz,M、N、P为电场中的三个点,M点的坐标(0,a,0),N点的坐标为(a,0,0),P点的坐标为(a,| a |
| 2 |
| a |
| 2 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 在如图所示的直角坐标系xyz所在的区域内,存在电场强度为E的匀强电场和磁感强度为B的匀强磁场.已知从坐标原点O沿x轴的正方向射入质子,穿过这区域时未发生偏转.设重力可忽略不计,则这区域中的E和B的方向可能是( )
在如图所示的直角坐标系xyz所在的区域内,存在电场强度为E的匀强电场和磁感强度为B的匀强磁场.已知从坐标原点O沿x轴的正方向射入质子,穿过这区域时未发生偏转.设重力可忽略不计,则这区域中的E和B的方向可能是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,直角坐标系的ox轴水平,oy轴竖直;M点坐标为(-0.3m,0)、N点坐标为(-0.2m,0);在-0.3m≤X≤-0.2m的长条形范围内存在竖直方向的匀强电场E0;在X≥0的范围内存在竖直向上的匀强电场,场强为E=20N/C;在第一象限的某处有一圆形的匀强磁场区,磁场方向垂直纸面向外,磁感应强度B=2.5T.有一带电量q=+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场,恰好垂直经过y轴上的P点(图中未画出,yP>0),而后微粒经过第一象限某处的圆形磁场区,击中x轴上的Q点,速度方向与x轴正方向夹角为60°.g取10m/s2.求:
如图所示,直角坐标系的ox轴水平,oy轴竖直;M点坐标为(-0.3m,0)、N点坐标为(-0.2m,0);在-0.3m≤X≤-0.2m的长条形范围内存在竖直方向的匀强电场E0;在X≥0的范围内存在竖直向上的匀强电场,场强为E=20N/C;在第一象限的某处有一圆形的匀强磁场区,磁场方向垂直纸面向外,磁感应强度B=2.5T.有一带电量q=+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场,恰好垂直经过y轴上的P点(图中未画出,yP>0),而后微粒经过第一象限某处的圆形磁场区,击中x轴上的Q点,速度方向与x轴正方向夹角为60°.g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,直角坐标系xOy位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的磁感应强度为B,方向垂直xOy平面向里,电场线平行于y轴.一质量为m、电荷量为q的带正电的小球,从y轴上的A点水平向右抛出,经x轴上的M点进入电场和磁场,恰能做匀速圆周运动,从x轴上的N点第一次离开电场和磁场,MN之间的距离为L,小球过M点时的速度方向与x轴正方向夹角为θ.不计空气阻力,重力加速度为g,求:
如图所示,直角坐标系xOy位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的磁感应强度为B,方向垂直xOy平面向里,电场线平行于y轴.一质量为m、电荷量为q的带正电的小球,从y轴上的A点水平向右抛出,经x轴上的M点进入电场和磁场,恰能做匀速圆周运动,从x轴上的N点第一次离开电场和磁场,MN之间的距离为L,小球过M点时的速度方向与x轴正方向夹角为θ.不计空气阻力,重力加速度为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:
 在如图所示的直角坐标系中,第一象限内存在着一个水平宽度为L(ON>L≥
在如图所示的直角坐标系中,第一象限内存在着一个水平宽度为L(ON>L≥| ON |
| 2 |
2
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com