

分析 (1)要使粒子从x轴射出,粒子在磁场中运动时间t为其周期的一半,必须满足t≤$\frac{{T}_{0}}{2}$.
(2)若粒子从B点沿y轴正方形射出磁场,画出运动轨迹,由周期性写出粒子运动时间与周期的关系,从而求解.由几何关系求出轨迹半径,由牛顿第二定律求v.
解答 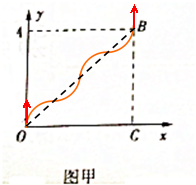 解:(1)粒子在磁场中运动时,有 qvB0=m$\frac{{v}^{2}}{r}$,则 r=$\frac{mv}{q{B}_{0}}$
解:(1)粒子在磁场中运动时,有 qvB0=m$\frac{{v}^{2}}{r}$,则 r=$\frac{mv}{q{B}_{0}}$
运动周期 T=$\frac{2πr}{v}$=$\frac{2πm}{q{B}_{0}}$
若粒子从x轴射出,则粒子在磁场中运动时间 t=$\frac{T}{2}$=$\frac{πm}{q{B}_{0}}$
磁场变化周期T0必须满足:t≤$\frac{{T}_{0}}{2}$
解得 T0≥$\frac{2πm}{q{B}_{0}}$.
(2)若粒子从B点沿y轴正方形射出磁场,则
①粒子在磁场中运动的时间 t=nT0,n=1,2,3,…
又 t=2n•$\frac{T}{4}$
联立解得磁场变化的周期 T0=$\frac{πm}{q{B}_{0}}$
②设粒子的轨迹半径为R.由几何关系应有:2n•$\sqrt{2}$R=$\sqrt{2}$l
故 R=$\frac{l}{2n}$,n=1,2,3,…
由r=$\frac{mv}{q{B}_{0}}$得
粒子射入磁场的速度 v=$\frac{q{B}_{0}l}{2mn}$,n=1,2,3,….
答:(1)若粒子从x轴射出,磁场变化周期T0的取值范围为T0≥$\frac{2πm}{q{B}_{0}}$.
(2)若粒子从B点沿y轴正方形射出磁场,求:
①磁场变化的周期T0为$\frac{πm}{q{B}_{0}}$.
②粒子射入磁场的速度v的取值为$\frac{q{B}_{0}l}{2mn}$,n=1,2,3,….
点评 带电粒子在复合场中的运动,重点就是运动分析,要着重掌握圆周运动的规律,还有相应的数学知识,做到能准确找出圆心,明确运动的轨迹.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:选择题
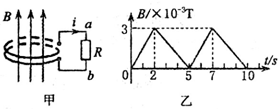 如图甲,匝数n=2的金属线圈(电阻不计)围成的面积为10cm2,线圈与R=2Ω的电阻连接,置于竖直向上、均匀分布的磁场中.磁场与线圈平面垂直,磁感应强度为B.B-t关系如图乙,规定感应电流i从a经过R到b的方向为正方向.忽略线圈的自感影响.则下列i-t关系图正确的是( )
如图甲,匝数n=2的金属线圈(电阻不计)围成的面积为10cm2,线圈与R=2Ω的电阻连接,置于竖直向上、均匀分布的磁场中.磁场与线圈平面垂直,磁感应强度为B.B-t关系如图乙,规定感应电流i从a经过R到b的方向为正方向.忽略线圈的自感影响.则下列i-t关系图正确的是( )| A. | 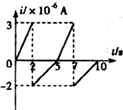 | B. | 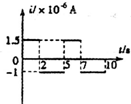 | C. | 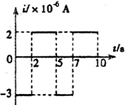 | D. | 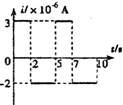 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
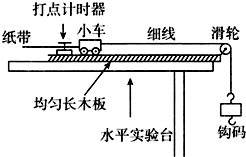 利用如图所示装置可以做力学中的许多实验.
利用如图所示装置可以做力学中的许多实验.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
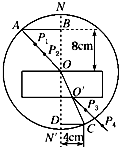 某同学做测定玻璃折射率实验时,由于没有量角器,在完成了光路图以后,他以O点为圆心,以10.00cm为半径画圆,分别交线段OA于A点,交OO′连线的延长线于C点,过A点作法线NN′的垂线AB交NN′于B点,过C点作法线NN′的垂线CD交NN′于D点,如图所示.用刻度尺量得OB=8.00cm,CD=4.00cm,由此可得出该玻璃的折射率n=1.5,该玻璃临界角的正弦值为0.67.
某同学做测定玻璃折射率实验时,由于没有量角器,在完成了光路图以后,他以O点为圆心,以10.00cm为半径画圆,分别交线段OA于A点,交OO′连线的延长线于C点,过A点作法线NN′的垂线AB交NN′于B点,过C点作法线NN′的垂线CD交NN′于D点,如图所示.用刻度尺量得OB=8.00cm,CD=4.00cm,由此可得出该玻璃的折射率n=1.5,该玻璃临界角的正弦值为0.67.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
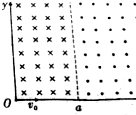 如图所示,在第一象限内,0<x≤a的区域中有垂直于纸面向里的匀强磁场,已知磁感应强度的大小为B1;x>a的区域中有垂直于纸面向外的匀强磁场,在原点O处有一小孔,一束质量为m、电荷量为q带正电的粒子,沿着x轴方向以不同的速率经小孔射入磁场,且速率最大的粒子在0<x≤a区域内运动的时候转过的圆心角为60°,它最终从x轴离开磁场时速度方向与x轴负方向的夹角为30°,不计粒子重力,求:
如图所示,在第一象限内,0<x≤a的区域中有垂直于纸面向里的匀强磁场,已知磁感应强度的大小为B1;x>a的区域中有垂直于纸面向外的匀强磁场,在原点O处有一小孔,一束质量为m、电荷量为q带正电的粒子,沿着x轴方向以不同的速率经小孔射入磁场,且速率最大的粒子在0<x≤a区域内运动的时候转过的圆心角为60°,它最终从x轴离开磁场时速度方向与x轴负方向的夹角为30°,不计粒子重力,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 为了较准确地测量某电子元件的电阻,某实验小组做如下测量:
为了较准确地测量某电子元件的电阻,某实验小组做如下测量:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 有一个推矿泉水瓶的游戏节目,规则是:选手们从起点开始用力推瓶一段时间后,放手让瓶向前滑动,若瓶最后停在桌上有效区域内,视为成功;若瓶最后未停在桌上有效区域内或在滑行过程中倒下,均视为失败.其简化模型如图所示,AC是长度为L1=5m的水平桌面,选手们可将瓶子放在A点,从A点开始用一恒定不变的水平推力推瓶,BC为有效区域.已知BC长度L2=1m,瓶子质量m=0.5kg,瓶子与桌面间的动摩擦因数μ=0.4.某选手作用在瓶子上的水平推力F=20N,瓶子沿AC做直线运动,假设瓶子可视为质点,g取10m/s2,那么该选手要想游戏获得成功,试问:
有一个推矿泉水瓶的游戏节目,规则是:选手们从起点开始用力推瓶一段时间后,放手让瓶向前滑动,若瓶最后停在桌上有效区域内,视为成功;若瓶最后未停在桌上有效区域内或在滑行过程中倒下,均视为失败.其简化模型如图所示,AC是长度为L1=5m的水平桌面,选手们可将瓶子放在A点,从A点开始用一恒定不变的水平推力推瓶,BC为有效区域.已知BC长度L2=1m,瓶子质量m=0.5kg,瓶子与桌面间的动摩擦因数μ=0.4.某选手作用在瓶子上的水平推力F=20N,瓶子沿AC做直线运动,假设瓶子可视为质点,g取10m/s2,那么该选手要想游戏获得成功,试问:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
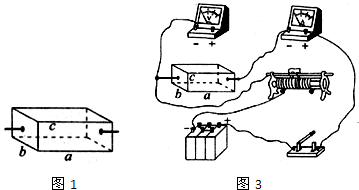
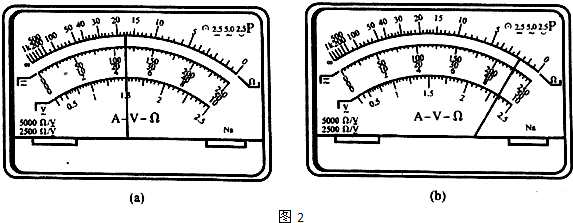
| 组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| U/V | 5.1 | 5.8 | 7.0 | 8.1 | 9.0 | 10.0 | 11.0 |
| I/mA | 2.9 | 3.3 | 4.0 | 5.0 | 5.1 | 5.7 | 6.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com