
分析 人造地球卫星绕地球做匀速圆周运动,根据人造卫星的万有引力等于向心力,列式求出线速度、周期和向心力的表达式求解.
解答 解:(1)人造地球卫星绕地球做匀速圆周运动,根据人造卫星的万有引力等于向心力,
$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,r=2R
v=$\sqrt{\frac{GM}{r}}$=$\sqrt{\frac{GM}{2R}}$,
(2)根据人造卫星的万有引力等于向心力,
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
T=2π$\sqrt{\frac{{r}^{3}}{GM}}$=4π$\sqrt{\frac{{2R}^{3}}{GM}}$,
答:(1)卫星运动速度的大小是$\sqrt{\frac{GM}{2R}}$;
(2)卫星运动的周期是4π$\sqrt{\frac{{2R}^{3}}{GM}}$.
点评 本题关键根据人造卫星的万有引力等于向心力,灵活的选择向心力的表达式是我们顺利解决此类题目的基础.我们要按照不同的要求选择不同的公式来进行求解.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中物理 来源: 题型:解答题
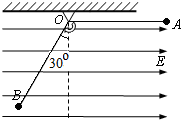 如图所示,在水平向右的匀强电场中,用长为L不可伸长的绝缘细线拴住一质量为m,带电荷量为q的小球,线的上端固定于O点.细线与竖直方向成30°角时静止释放小球,小球开始摆动,当摆到A点时速度为零,此时OA恰好处于水平状态,设整个过程中细线始终处于拉直状态,静电力常量为k,忽略空气阻力.
如图所示,在水平向右的匀强电场中,用长为L不可伸长的绝缘细线拴住一质量为m,带电荷量为q的小球,线的上端固定于O点.细线与竖直方向成30°角时静止释放小球,小球开始摆动,当摆到A点时速度为零,此时OA恰好处于水平状态,设整个过程中细线始终处于拉直状态,静电力常量为k,忽略空气阻力.查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | v=25 cm/s,向左传播 | B. | v=50 cm/s,向左传播 | ||
| C. | v=25 cm/s,向右传播 | D. | v=50 cm/s,向右传播 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{{4{π^2}R}}{g_0}$ | B. | $\frac{{4{π^2}(R+h)}}{g_0}$ | C. | $\frac{2πh}{R}\sqrt{\frac{h}{g_0}}$ | D. | $\frac{2π(R+h)}{R}\sqrt{\frac{R+h}{g_0}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
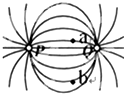
| A. | Ea>Eb方向相同 | B. | Ea<Eb 方向相同 | C. | Ea<Eb 方向不同 | D. | Ea>Eb方向不同 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 在高速公路的拐弯处,路面造得外高内低,即当车向右拐弯时,司机左侧的路面比右侧的要高一些,路面与水平面间的夹角为θ,设拐弯路段是半径为R的圆弧,要使车速为v时车轮与路面之间的横向(即垂直于前进方向)摩擦力等于零,θ应满足( )
在高速公路的拐弯处,路面造得外高内低,即当车向右拐弯时,司机左侧的路面比右侧的要高一些,路面与水平面间的夹角为θ,设拐弯路段是半径为R的圆弧,要使车速为v时车轮与路面之间的横向(即垂直于前进方向)摩擦力等于零,θ应满足( )| A. | sinθ=$\frac{{v}^{2}}{Rg}$ | B. | tanθ=$\frac{{v}^{2}}{Rg}$ | C. | sin2θ=$\frac{2{v}^{2}}{Rg}$ | D. | cotθ=$\frac{{v}^{2}}{Rg}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
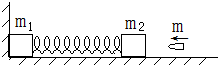 如图所示,固定在轻质弹簧两端质量分别是m1=m、m2=$\frac{3}{4}$m的两个物体置于光滑水平面上,m1靠在光滑竖直墙上,现有一颗m3=$\frac{1}{4}$m的子弹水平射入m2中,使弹簧压缩最短时具有的弹性势能为E,然后m1和m2都将向右运动,试求:
如图所示,固定在轻质弹簧两端质量分别是m1=m、m2=$\frac{3}{4}$m的两个物体置于光滑水平面上,m1靠在光滑竖直墙上,现有一颗m3=$\frac{1}{4}$m的子弹水平射入m2中,使弹簧压缩最短时具有的弹性势能为E,然后m1和m2都将向右运动,试求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | F与r2成反比 | B. | F与r2成正比 | C. | F与r3成正比 | D. | F与r4成正比 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com