
火星的球半径是地球半径的1/2,火星质量是地球质量的1/10,忽略火星的自转,如果地球上质量为60㎏的人到火星上去,则此人在火星表面的质量是_______㎏,所受的重力是______N;在火星表面由于火星的引力产生的加速度是________m/s;在地球表面上可举起60㎏杠铃的人,到火星上用同样的力,可以举起质量_______㎏的物体。g取9.8 m/s2
科目:高中物理 来源: 题型:单选题
均匀分布在地球赤道平面上空的三颗同步通信卫星能够实现除地球南北极等少数地区外的“全球通信”。已知地球半径为R,地球表面的重力加速度为g,同步卫星所在轨道处的重力加速度为g′,则三颗卫星中任意两颗卫星间距离为
A. | B.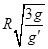 | C.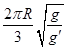 | D.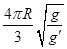 |
查看答案和解析>>
科目:高中物理 来源: 题型:单选题
火星探测项目是我国继神舟载人航天工程、嫦娥探月工程之后又一个重大太空探索项目.假设火星探测器在火星表面附近圆形轨道运行的周期为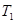 ,神舟飞船在地球表面附近的圆形轨道运行周期为
,神舟飞船在地球表面附近的圆形轨道运行周期为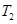 ,火星质量与地球质量之比为p,火星半径与地球半径之比为q,则
,火星质量与地球质量之比为p,火星半径与地球半径之比为q,则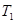 与
与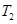 之比为( )
之比为( )
A.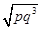 | B.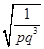 | C.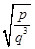 | D.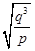 |
查看答案和解析>>
科目:高中物理 来源: 题型:单选题
宇宙中有这样一种三星系统,系统由两个质量为m的小星体和一个质量为M的大星体组成,两个小星体围绕大星体在同一圆形轨道上运行,轨道半径为r.关于该三星系统的说法中正确的是( )
①在稳定运行情况下,大星体提供两小星体做圆周运动的向心力 ②在稳定运行情况下,大星体应在小星体轨道中心,两小星体在大星体相对的两侧 ③小星体运行的周期为 ④大星体运行的周期为
④大星体运行的周期为
| A.①③ | B.②③ |
| C.①④ | D.②④ |
查看答案和解析>>
科目:高中物理 来源: 题型:单选题
太阳系中的8大行星的轨道均可以近似看成圆轨道.下列4幅图是用来描述这些行星运动所遵从的某一规律的图象.图中坐标系的横轴是lg(T/T0),纵轴是lg(R/R0);这里T和R分别是行星绕太阳运行的周期和相应的圆轨道半径,T0和R0分别是水星绕太阳运行的周期和相应的圆轨道半径.下列4幅图中正确的是( )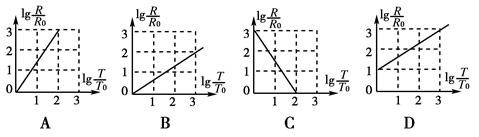
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
(4分)(2011?海南)2011年4月10日,我国成功发射第8颗北斗导航卫星,建成以后北斗导航卫星系统将包含多颗地球同步卫星,这有助于减少我国对GPS导航系统的依赖,GPS由运行周期为12小时的卫星群组成,设北斗星的同步卫星和GPS导航的轨道半径分别为R1和R2,向心加速度分别为a1和a2,则R1:R2= a1:a2= .(可用根式表示)
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
(8分)一星球的半径为R,为了测量该星球两极和赤道的重力加速度及星球自转角速度,某人用小球在该星球表面做了以下实验:(不计小球在运动的过程中所受阻力)
①在该星球的两极(相当于地球的南极和北极),以初速度v0(相对地面)从h高处将一小球水平抛出,小球触地时速度与水平方向成α角.则测量的该星球两极的重力加速度为 ;
②在该星球的赤道上(相当于地球的赤道),同样以速度v0(相对地面)从h高处将一小球水平抛出,小球触地时速度与水平方向成β角.该星球赤道上的重力加速度为 ;该星球的自转角速度为 .
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即 k是一个对所有行星都相同的常量.将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式.已知引力常量为G,太阳的质量为M太.
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立.经测定月地距离为3.84×108m,月球绕地球运动的周期为2.36×106s,试计算地球的质量M地.(G=6.67×10-11Nm2/kg2,结果保留一位有效数字)
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
(10分)某同学是一位航天科技爱好者,当他从新闻中得知,中国航天科技集团公司将在2010年底为青少年发射第一颗科学实验卫星——“希望一号”卫星(代号XW-1)时,他立刻从网上搜索有关“希望一号”卫星的信息,其中一份资料中给出该卫星运行周期10.9min。他根据所学知识计算出绕地卫星的周期不可能小于83min,从而断定此数据有误。
已知地球的半径R=6.4×106m,地球表面的重力加速度g=10m/s2。请你通过计算说明为什么发射一颗周期小于83min的绕地球运行的人造地球卫星是不可能的。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com