
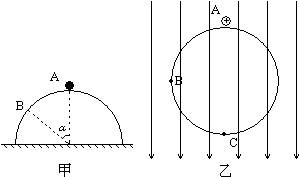
 如图甲所示,一个光滑的小球放在光滑半球上,半球固定,小球受到轻微扰动后,会在B点离开球面,离开时的角度为α.如图乙所示,一个半径为R的光滑绝缘的圆环固定在竖直平面内,电场强度为E,方向竖直向下.一质量为m,带电量为q的小球从A点由静止开始从左边滑下.
如图甲所示,一个光滑的小球放在光滑半球上,半球固定,小球受到轻微扰动后,会在B点离开球面,离开时的角度为α.如图乙所示,一个半径为R的光滑绝缘的圆环固定在竖直平面内,电场强度为E,方向竖直向下.一质量为m,带电量为q的小球从A点由静止开始从左边滑下.分析 (1)对小球运动过程应用动能定理,再对分离点应用牛顿第二定律即可根据支持力为零求解;
(2)首先由小球偏转方向应用左手定则判断磁感应强度方向;然后对小球运动过程应用动能定理,再对任一点应用牛顿第二定律即可求得磁感应强度范围,然后根据表达式求得任一点磁感应强度最小值的最大值;
(3)根据小球运动过程的受力情况及做功情况求解.
解答 解:(1)小球运动过程受重力、支持力和电场力作用;小球下滑过程支持力不做功,重力、电场力做正功,故有动能定理可得:小球的速度不断增大;
那么,小球运动的向心力增大;随着小球下滑,重力、电场力在径向的分量逐渐减小,到B点时减为零;
故小球不能紧贴圆弧下滑到水平位置B点处,当支持力为零,重力、电场力的径向分量正好等于向心力时,小球离开;
假设小球脱离轨道时小球的速度为v,且该点与A点的圆心角为θ,则有:
$(qE+mg)R(1-cosθ)=\frac{1}{2}m{v}^{2}$,$(qE+mg)cosθ=\frac{m{v}^{2}}{R}$;
所以,$cosθ=\frac{2}{3}$;
(2)由小球偏转方向,根据左手定则可知:必须加一个垂直纸面向里的磁场;
当小球在与A点的圆心角为α时,由动能定理可得:$(qE+mg)R(1-cosα)=\frac{1}{2}mv{′}^{2}$
由牛顿第二定律可得:$(qE+mg)cosα+Bv′q≥\frac{m{v′}^{2}}{R}$;
所以,Bv′q≥2(qE+mg)(1-cosα)-(qE+mg)cosα=(qE+mg)(2-3cosα);
所以,$B≥\frac{(qE+mg)(2-3cosα)}{qv′}=\frac{1}{q}\sqrt{\frac{m(qE+mg)(2-3cosα)^{2}}{2R(1-cosα)}}$;
故cosα=-1时,$\frac{1}{q}\sqrt{\frac{m(qE+mg)(2-3cosα)^{2}}{2R(1-cosα)}}$取得最大值$\frac{5}{2q}\sqrt{\frac{m(qE+mg)}{R}}$;
所以,B至少是$\frac{5}{2q}\sqrt{\frac{m(qE+mg)}{R}}$才能使小球到达A点的正下方C点;
(3)由小球运动过程的受力情况及各力做功情况可知:小球从A到C和从C到A的运动完全对称,故小球能再次通过A点,且通过A点速度还是零.
答:(1)小球从不能紧贴圆弧下滑到水平位置B点处,它大概在与A点的圆心角的余弦值为$\frac{2}{3}$的位置离开;
(2)如果加一个垂直纸面的磁场B,B至少是$\frac{5}{2q}\sqrt{\frac{m(qE+mg)}{R}}$才能使小球到达A点的正下方C点,磁场的方向垂直纸面向里;
(3)在该磁场的作用下,能再次通过A点,且通过A点的速度大小还是零.
点评 带电粒子的运动问题,加速电场一般由动能定理或匀加速运动规律求解;偏转电场由类平抛运动规律求解;磁场中的运动问题则根据圆周运动规律结合几何条件求解.


科目:高中物理 来源: 题型:计算题
 如图所示闭合电路,电源电动势E=1.5V,内电阻r=0.1Ω,外电路电阻R=1.4Ω.求:
如图所示闭合电路,电源电动势E=1.5V,内电阻r=0.1Ω,外电路电阻R=1.4Ω.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 只要知道气体的摩尔体积和阿伏伽德罗常数,就可以计算出气体分子的体积 | |
| B. | 悬浮在液体中的固体颗粒越大,布朗运动就越明显 | |
| C. | 一定质量理想气体,保持气体的压强不变,温度越高,体积越大 | |
| D. | 第二类永动机不可能制成是因为它违反了能量守恒定律 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,半径为R=1.6m的圆轨道ABC固定在竖直平面内,在C与水平地面平滑连接.一个质量m=0.5kg的小球经压缩的弹簧弹射出去后,通过最高点A时对轨道的压力大小等于其重力的3倍.不计一切摩擦和空气阻力,g取10m/s2.求:
如图所示,半径为R=1.6m的圆轨道ABC固定在竖直平面内,在C与水平地面平滑连接.一个质量m=0.5kg的小球经压缩的弹簧弹射出去后,通过最高点A时对轨道的压力大小等于其重力的3倍.不计一切摩擦和空气阻力,g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 10 m | B. | 20 m | C. | 30 m | D. | 40 m |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
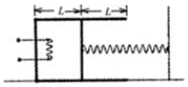 如图所示,长为2L=20cm内壁光滑的气缸放在水面上,气缸和活塞气密性良好且绝热,活塞的横截面积为s=10cm2,活塞与墙壁之间连接一根劲度系数为k=50N/m的轻弹簧,当缸内气体温度为T0=27℃时,活塞恰好位于气缸的中央位置,且经弹簧处于原长状态.已知气缸与活塞的总质量为M=4kg,气缸与水平面间的动摩擦因数为μ=0.2,大气压强为p0=1×105Pa,重力加速度为g=10m/s2.现用电热丝对缸内气体缓慢加热,当活塞移到气缸最右端时,缸内气温是多少?
如图所示,长为2L=20cm内壁光滑的气缸放在水面上,气缸和活塞气密性良好且绝热,活塞的横截面积为s=10cm2,活塞与墙壁之间连接一根劲度系数为k=50N/m的轻弹簧,当缸内气体温度为T0=27℃时,活塞恰好位于气缸的中央位置,且经弹簧处于原长状态.已知气缸与活塞的总质量为M=4kg,气缸与水平面间的动摩擦因数为μ=0.2,大气压强为p0=1×105Pa,重力加速度为g=10m/s2.现用电热丝对缸内气体缓慢加热,当活塞移到气缸最右端时,缸内气温是多少?查看答案和解析>>
科目:高中物理 来源: 题型:计算题
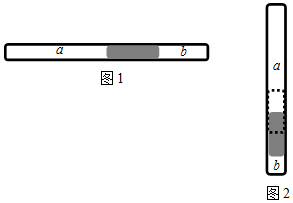 如图1所示,长度为4L、内壁光滑且两端封口的细玻璃管水平静止放置,一段长度为L的水银柱将管内密封的理想气体分隔成长度为2L和L的两部分a和b.
如图1所示,长度为4L、内壁光滑且两端封口的细玻璃管水平静止放置,一段长度为L的水银柱将管内密封的理想气体分隔成长度为2L和L的两部分a和b.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 电流方向将发生改变 | |
| B. | 通过线圈的磁通量达到最大值 | |
| C. | 通过线圈的磁通量的变化率达到最大值 | |
| D. | 线圈的电动势为零 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com