
 如图所示,一匀强电场平行于正方形区域ABCD,AB边水平,BC边垂直,A、B、C三点的电势分别为6V、2V、-2V.一质量为m,电量大小为q的带电微粒,从P点射入该电场区,恰好沿水平直线运动,下列判断正确的是( )
如图所示,一匀强电场平行于正方形区域ABCD,AB边水平,BC边垂直,A、B、C三点的电势分别为6V、2V、-2V.一质量为m,电量大小为q的带电微粒,从P点射入该电场区,恰好沿水平直线运动,下列判断正确的是( )| A. | 微粒带正电 | B. | 微粒做匀速直线运动 | ||
| C. | 电场强度的大小为$\frac{\sqrt{2}mg}{q}$ | D. | 微粒的电势能逐渐减少 |
分析 依据匀强电场的特点,结合A、B、C三点的电势分别为6V、2V、-2V可得电场的分向,由带电微粒,从P点射入该电场区,恰好沿水平直线运动,则重力与电场力的合力必定与运动轨迹共线,由力的平行四边形定则可得电场强度.
解答 解:A、正方形区域ABCD,则有:UAD=UBC=4V,故有D点的电势为2V,故对角线BD为等势线,故电场线方向为从A指向C,微粒恰好沿水平直线运动,则重力与电场力的合力必定沿着水平方向,故电场力沿着电场线的反方向,故微粒带负电,故A错误;
B、微粒仅受重力和电场力作用,合力不可能为零,故不可能做匀速直线运动,故B错误;
C、重力与电场力的合力必定沿着水平方向,由平行四边形定则可得,Eq=$\sqrt{2}mg$,故E=$\frac{\sqrt{2}mg}{q}$,故C正确;
D、电场力做负功,电势能增加,故D错误.
故选:C.
点评 知道匀强电场中相同方向相等距离的电势差相等;电场线与等势线垂直,并且由高电势指向低电势;微粒恰好沿水平直线运动,则重力与电场力的合力必定与运动轨迹共线,这几点很重要.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 微观粒子的动量不可能确定 | |
| B. | 微观粒子的坐标不可能确定 | |
| C. | 微观粒子的动量和坐标不可能同时确定 | |
| D. | 不确定性关系不仅适用于电子和光子,也适用于其他微观粒子 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
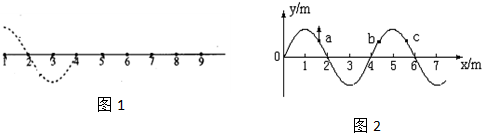
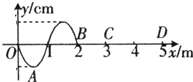 一列简谐横波沿x轴正方向传播,在t=0时波传播到x轴上的质点B,在它左侧的质点A恰好位于负向最大位移处,如图所示,在t=0.6s时,质点A第三次到达正向最大位移处,则( )
一列简谐横波沿x轴正方向传播,在t=0时波传播到x轴上的质点B,在它左侧的质点A恰好位于负向最大位移处,如图所示,在t=0.6s时,质点A第三次到达正向最大位移处,则( )| A. | 该波的速度等于5m/s | |
| B. | t=0.6s时,质点C在平衡位置处且向下运动 | |
| C. | t=0.6s时,质点C在平衡位置处且向上运动 | |
| D. | 当质点D第一次到达正向在最大位移处时,质点B恰好在平衡位置且向下运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{1}{2}$mgv0 | B. | mg$\sqrt{gh}$ | C. | mg$\sqrt{2gh}$ | D. | mgv0 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
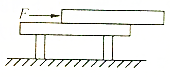 如图所示,一块质量为m,长为L的均匀长方形木块放在水平桌面上,木块与桌面间动摩擦因素为μ.现用水平力F推木块,当木块经过图示位置(木块伸出桌外$\frac{2}{5}$L)时,桌面对它的摩擦力的大小为多少?
如图所示,一块质量为m,长为L的均匀长方形木块放在水平桌面上,木块与桌面间动摩擦因素为μ.现用水平力F推木块,当木块经过图示位置(木块伸出桌外$\frac{2}{5}$L)时,桌面对它的摩擦力的大小为多少?查看答案和解析>>
科目:高中物理 来源: 题型:多选题
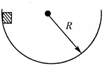 质量为m的物体沿着半径为R的半球金属球壳滑到最低点时的速度大小为v,如图所示.若物体与球壳之间的摩擦因数为μ,则物体在最低点时的( )
质量为m的物体沿着半径为R的半球金属球壳滑到最低点时的速度大小为v,如图所示.若物体与球壳之间的摩擦因数为μ,则物体在最低点时的( )| A. | 向心加速度为$\frac{{v}^{2}}{R}$ | B. | 向心力为m(g+$\frac{{v}^{2}}{R}$) | ||
| C. | 对球壳的压力为$\frac{m{v}^{2}}{R}$ | D. | 受到的摩擦力为μm(g+$\frac{{v}^{2}}{R}$) |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,某轻杆一端固定一个质量为m,且大小可忽略不计的小球,另一端可绕O点在竖直平面内自由转动,不计转轴的摩擦,杆长为R,重力加速度为g.则下列说法中正确的是( )
如图所示,某轻杆一端固定一个质量为m,且大小可忽略不计的小球,另一端可绕O点在竖直平面内自由转动,不计转轴的摩擦,杆长为R,重力加速度为g.则下列说法中正确的是( )| A. | 小球通过最低点时,杆对小球的弹力的方向可能竖直向下 | |
| B. | 小球通过最高点时小球的速度一定为$\sqrt{gR}$ | |
| C. | 若轻杆经过水平位置时小球的速度为v,则杆对球的弹力大小为$m\frac{v^2}{R}$ | |
| D. | 若轻杆经过水平位置时小球的速度为v,则杆对球的弹力大小为$m\sqrt{{{({\frac{v^2}{R}})}^2}+{g^2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com