
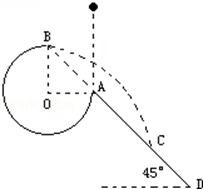
 如图所示,竖直平面内的$\frac{3}{4}$圆弧形光滑轨道半径为R,A端与圆心O等高,AD为与水平方向成45°角的斜面.B端在O的正上方.一个小球在A点正上方由静止开始释放,自由下落至A点后进入圆形轨道并恰能到达B点,求:
如图所示,竖直平面内的$\frac{3}{4}$圆弧形光滑轨道半径为R,A端与圆心O等高,AD为与水平方向成45°角的斜面.B端在O的正上方.一个小球在A点正上方由静止开始释放,自由下落至A点后进入圆形轨道并恰能到达B点,求:分析 (1)由牛顿第二定律求得在B处的速度;
(2)由平抛运动位移规律,根据几何关系求得平抛运动时间,然后根据平抛运动速度规律求解末速度;
(3)根据平抛运动位移规律求得任意时刻到斜面距离的表达式,进而求得最大值.
解答 解:(1)小球恰能到达B点,那么对小球在B点应用牛顿第二定律可得:$mg=\frac{m{{v}_{B}}^{2}}{R}$,所以,${v}_{B}=\sqrt{gR}$;
(2)小球从B到C做平抛运动,故有$y=\frac{1}{2}g{t}^{2}$,x=vBt;由几何关系可知:x=y,所以,$t=\sqrt{\frac{2R}{g}}$,那么,小球在C点时的竖直分速度${v}_{Cy}=gt=\sqrt{2gR}$,
所以,小球在C点的速度${v}_{C}=\sqrt{3gR}$;
(3)小球从B点到达C点过程中任意时刻离BD的距离$d=\frac{|x-y|}{\sqrt{2}}=\frac{|\sqrt{gR}t-\frac{1}{2}g{t}^{2}|}{\sqrt{2}}$=$\frac{|(\sqrt{\frac{g}{2}}t-\sqrt{\frac{R}{2}})^{2}-\frac{R}{2}|}{\sqrt{2}}$,
所以,当$t=\sqrt{\frac{R}{g}}$时,x=R,$y=\frac{1}{2}R$,小球从B点到达C点过程中离斜面最远,
答:(1)到达B点时小球的速度为$\sqrt{gR}$;
(2)小球落到斜面上C点时的速度大小为$\sqrt{3gR}$;
(3)小球从B点到达C点过程中$t=\sqrt{\frac{R}{g}}$时离斜面最远.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:多选题
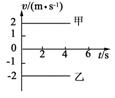 如图所示为甲、乙两质点运动的v-t图象.对于甲、乙两质点的运动情况,下列说法中正确的是 ( )
如图所示为甲、乙两质点运动的v-t图象.对于甲、乙两质点的运动情况,下列说法中正确的是 ( )| A. | 两个质点运动的速度相同 | |
| B. | 两个质点的运动方向相反 | |
| C. | 相同时间内,两质点运动的位移相同 | |
| D. | 若两质点同时从同一地点出发,它们间的距离会越来越大 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
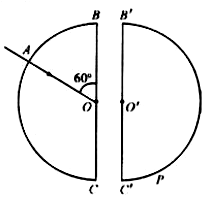 如图所示,两块半径均为R的半圆形玻璃砖平行对称放置,沿竖直方向的两条直径BC、B′C′相互平行,两圆心之间的距离为$\frac{R}{3}$.一束单色光正对圆心O从A点射入左侧的玻璃砖,最后从右侧玻璃砖上的P点射出.已知∠AOB=60°,玻璃折射率为n=$\sqrt{3}$,若不考虑光在各个界面的反射.
如图所示,两块半径均为R的半圆形玻璃砖平行对称放置,沿竖直方向的两条直径BC、B′C′相互平行,两圆心之间的距离为$\frac{R}{3}$.一束单色光正对圆心O从A点射入左侧的玻璃砖,最后从右侧玻璃砖上的P点射出.已知∠AOB=60°,玻璃折射率为n=$\sqrt{3}$,若不考虑光在各个界面的反射.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,物体在离斜面底端L处由静止开始下滑,然后滑上由小圆弧(长度忽略)与斜面连接的水平面上,水平面足够长,动摩擦因数为0.5.若斜面是光滑的,物体在水平面上滑行的距离为s1;若斜面粗糙,动摩擦因数也为0.5,物体在水平面上滑行的距离为s2.斜面倾角为37°,求s1:s2为多少?(已知sin37°=0.6,cos37°=0.8)
如图所示,物体在离斜面底端L处由静止开始下滑,然后滑上由小圆弧(长度忽略)与斜面连接的水平面上,水平面足够长,动摩擦因数为0.5.若斜面是光滑的,物体在水平面上滑行的距离为s1;若斜面粗糙,动摩擦因数也为0.5,物体在水平面上滑行的距离为s2.斜面倾角为37°,求s1:s2为多少?(已知sin37°=0.6,cos37°=0.8)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,木块A放在木板B的左上端,用恒力F将A拉至B的右端,第1次将B固定在地面上,木块A获得的动能为Ek;第2次可以让B在光滑的地面上自由的滑动,木块A获得的动能为Ek′.比较两次木块A获得的动能,则( )
如图所示,木块A放在木板B的左上端,用恒力F将A拉至B的右端,第1次将B固定在地面上,木块A获得的动能为Ek;第2次可以让B在光滑的地面上自由的滑动,木块A获得的动能为Ek′.比较两次木块A获得的动能,则( )| A. | Ek<Ek′ | B. | Ek=Ek′ | C. | Ek>Ek′ | D. | 无法确定 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 北京时间5月2日凌晨0时06分,中国在西昌卫星发射中心用“长征二号乙”运载火箭,将“中星十一号”通信卫星顺利发射升空,并成功送入预定转移轨道.如图是火箭点火升空瞬间时的照片.在这一瞬间关于火箭的速度和加速度的判断,下列说法正确的是( )
北京时间5月2日凌晨0时06分,中国在西昌卫星发射中心用“长征二号乙”运载火箭,将“中星十一号”通信卫星顺利发射升空,并成功送入预定转移轨道.如图是火箭点火升空瞬间时的照片.在这一瞬间关于火箭的速度和加速度的判断,下列说法正确的是( )| A. | 火箭的速度为0,但加速度不为0 | B. | 火箭的速度很大,加速度也很大 | ||
| C. | 火箭的速度为0,所以加速度也为0 | D. | 火箭的速度很大,但加速度很小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com