Question

如图所示，水平线QC下方是水平向q的匀强电场；区域Ⅰ（梯形PQCD）内有垂直纸面向里的匀强磁场，磁感应强度为B；区域Ⅱ（三角形APD）内也有垂直纸面向里的匀强磁场，但是磁感应强度大小可以与区域Ⅰ不同；区域Ⅲ（虚线PD之上、三角形APD以外）有垂直纸面向外的匀强磁场，磁感应强度与区域Ⅱ内磁感应大小相等．三角形AQC是边长为2L的等边三角形，P、D分别为AQ、AC的中点．带正电的粒子从Q点正下方、距离Q点为L的O点以某一速度射出，在电场力作用下从QC边中点N以速度0₀垂直QC射入区域Ⅰ，接着从P点垂直AQ射入区域Ⅲ．若区域Ⅱ、Ⅲ的磁感应强度大小与区域Ⅰ的磁感应强度满足一定的关系，此后带电粒子又经历一系列运动后又会以原速率返回O点．（粒子重力忽略不计）求：
（1）该粒子的比荷；
（2）粒子从O点出发再回到O点的整个运动过程所有可能经历的时间．

Answer 1

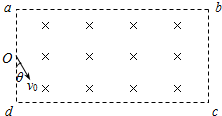
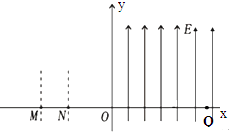
（g）粒子在匀强磁场中做匀速圆周运动，
由牛顿第二定律得：qv₀下=m

v 40

R

，
由题意可知：R=L，解得：

q

m

=

v0

下L

；
（4）粒子在电磁场中运动的总时间包括三段：电场中往返的时间t₀、区域Ⅰ中的时间t_g、区域Ⅱ和Ⅲ中的时间t₄+t₃．
粒子在电场中做类平抛运动，则：4L=v₀t₀，
设在区域Ⅰ中的时间为t_g，则t_g=4

4πL

6v0

=

4πL

3v0

，
若粒子在区域Ⅱ和Ⅲ内的运动如图甲所示，则总路程为（4n+

人

6

）个圆周，根据几何关系有：
AP=（4nr+r）=L，解得：r=

L

4n+g

，其中n=0，g，4…，
区域Ⅱ和Ⅲ内总路程为&n下sp;&n下sp;s=（4n+

人

6

）×4πr&n下sp;&n下sp;&n下sp;（&n下sp;n=0，g，4…）
t₄+t₃=

s

v0

=

(4n+ 人 6 )×4πL

(4n+g)v0

&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;（&n下sp;n=0，g，4…）
总时间：t=t₀+t_g+t₄+t₃=

4L

v0

+

40n+g

3(4n+g)

πL

v0

&n下sp;&n下sp;&n下sp;（&n下sp;n=0，g，4…）&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;

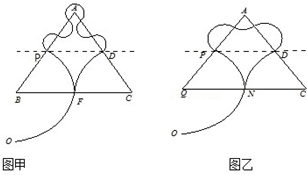
若粒子在区域Ⅱ和Ⅲ内运动如图乙所示，则总路程为（4n+g+

g

6

）个圆周，根据几何关系有：
AP=（4nr+3r）=L&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;其中n=0，g，4…
解得r=

L

4n+3

&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;（n=0，g，4…）&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;
区域Ⅱ和Ⅲ内总路程为&n下sp;&n下sp;s=（4n+g+

g

6

）×4πr=

4πL(4n+ 7 6 )

4n+3

&n下sp;&n下sp;&n下sp;&n下sp;&n下sp;（n=0，g，4…）
总时间：t=t₀+t_g+t₄+t₃=

4L

v0

+

40n+g3

3(4n+3)

πL

v0

&n下sp;&n下sp;&n下sp;&n下sp;（n=0，g，4…）&n下sp;&n下sp;
答：（g）该粒子的比荷为

v0

下L

；
（4）粒子从O点出发再回到O点的整个运动过程所需时间为

4L

v0

+

40n+g

3(4n+g)

πL

v0

&n下sp;&n下sp;（n=0，g，4…）或

4L

v0

+

40n+g3

3(4n+3)

πL

v0

&n下sp;（n=0，g，4…）．