
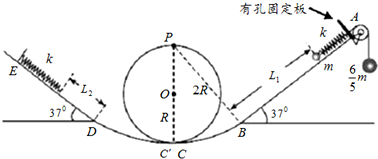
分析 (1)细线刚断时,小球的加速度大小根据牛顿第二定律求解;
(2)小球在经过C点时,在C点左右两边相当于分别在两个圆周上过最低点,根据重力和轨道的支持力的合力提供向心力,列式得到压力改变量与速度的关系式;小球恰好能完成竖直圆周运动时,在最高点由重力提供向心力,根据牛顿第二定律可求得最高点小球的速度.小球从最低点到最高点的过程中,机械能守恒,列出方程,联立即可求解.
(3)当小球能过顶,小球滑上左侧斜面轨道,压缩弹簧获得与初始线断时相同大小的加速度时,弹簧弹力为FN=$\frac{6}{5}$mg-mgsin37°,弹簧压缩量与右侧初始弹簧压缩量相同,则弹簧的弹性势能相等,整个过程机械能守恒,列式即可求解小球的速度.
解答 解:(1)线未断时,弹簧对小球m的弹力大小 ${F_N}=\frac{6}{5}mg-mgsin37°$
细线刚断时,小球的加速度$a=\frac{{{F_N}+mgsin37°}}{m}=\frac{{\frac{6}{5}mg}}{m}=\frac{6}{5}g$
(2)小球在经过C点时,在C点左右两边相当于分别在两个圆周上过最低点,
在右边:轨道对小球的支持力 FN1=Fn1+mg
得:${F_{N1}}=m\frac{v^2}{R_1}+mg$
在左边:轨道对小球的支持力 FN2=Fn2+mg
得:${F_{N2}}=m\frac{v^2}{R_2}+mg$
则小球对轨道的压力之差为:$△F={F_2}-{F_1}=m\frac{v^2}{R_2}-m\frac{v^2}{R_1}$
又 R1=2R,R2=R,
解得:$△F=m\frac{v^2}{2R}$
又小球从C点到P点过程中,机械能守恒,则得:$\frac{1}{2}m{v^2}-2mgR=\frac{1}{2}mv_0^2$
在最高点P时,由重力提供向心力,则有:$mg=m\frac{v_0^2}{R}$
联立解得:$△F=\frac{5}{2}mg$
(3)当小球能过顶,则小球滑上左侧斜面轨道,压缩弹簧获得与初始线断时相同大小的加速度时,弹簧弹力为${F_N}=\frac{6}{5}mg-mgsin37°=\frac{3}{5}mg$
即弹簧压缩量与右侧初始弹簧压缩量相同,均为$x=\frac{3mg}{5k}$
则弹簧的弹性势能相等,整个过程机械能守恒:
$mg{L_1}sin37°-mg({L_2}+\frac{3mg}{5k})sin37°=\frac{1}{2}mv_2^2$
解得:v2=$\frac{6}{5}g({L_1}-{L_2}-\frac{3mg}{5k})$
答:(1)细线刚断时,小球的加速度大小为$\frac{6}{5}$g;
(2)压力改变量为 $\frac{5}{2}$mg;
(3)小球冲上左侧轨道获得与初始线断相同的加速度时,小球的速度为$\frac{6}{5}g({L_1}-{L_2}-\frac{3mg}{5k})$.
点评 本题是复杂的力学问题,对于圆周运动,分析向心力的来源是关键,对于小球运动过程之中,要抓住机械能守恒,要具有解决综合问题的能力,需要加强这方面的练习.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
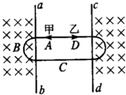 如图,ab和cd为两条相距较远的平行直线,ab的左侧和cd的右侧都有磁感应强度为B、方向垂直纸面向里的匀强磁场,闭合曲线是由两个半圆及与半圆相切的两条线段组成.甲、乙两带电体分别从图中的A、D两点以不同的初速度开始向两边运动,轨迹如图.它们在C点碰撞后结为一体向右运动.则下面说法正确的是(不计重力、阻力)( )
如图,ab和cd为两条相距较远的平行直线,ab的左侧和cd的右侧都有磁感应强度为B、方向垂直纸面向里的匀强磁场,闭合曲线是由两个半圆及与半圆相切的两条线段组成.甲、乙两带电体分别从图中的A、D两点以不同的初速度开始向两边运动,轨迹如图.它们在C点碰撞后结为一体向右运动.则下面说法正确的是(不计重力、阻力)( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 5 L | B. | 20 L | C. | 15 L | D. | 10 L |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
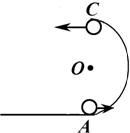 如图所示,竖直的半圆形轨道与水平面相切,轨道半径R=0.2m.质量m=200g的小球以某一速度正对半圆形轨道运动,A、B、C三点分别为圆轨道最低点、与圆心O等高点、最高点.小球过这三点的速度分别为vA=5m/s,vB=4m∠s,vC=3m/s,求:
如图所示,竖直的半圆形轨道与水平面相切,轨道半径R=0.2m.质量m=200g的小球以某一速度正对半圆形轨道运动,A、B、C三点分别为圆轨道最低点、与圆心O等高点、最高点.小球过这三点的速度分别为vA=5m/s,vB=4m∠s,vC=3m/s,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 球B一定向右做匀速运动.已知细绳与竖直方向的夹角为θ,求球B受到的风力,环A与水平细杆间的动摩擦因数.
球B一定向右做匀速运动.已知细绳与竖直方向的夹角为θ,求球B受到的风力,环A与水平细杆间的动摩擦因数.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
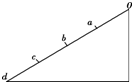 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )| A. | 质点由O到达各点的时间之比ta:tb:tc:td=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| B. | 质点通过各点的速率之比va:vb:vc:vd=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| C. | 在斜面上运动的平均速度$\overline{v}$=vb | |
| D. | 在斜面上运动的平均速度$\overline{v}$=$\frac{{v}_{d}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com