
 ��ͼ��ʾ�����ͨ��3���������ң�3�������Ľ��ΪO������OBˮƽ��B����վ��ˮƽ���ϵ�����Ϊm2=60kg��������������OA����ֱ����ļнǦ�=37�㣬��鼰�˶����ھ�ֹ״̬����֪����ˮƽ��֮��Ķ�Ħ������Ϊ��=0.3��sin37��=0.6��cos37��=0.8��ȡg=10m/s2�������Ħ�������ڻ���Ħ������Ҫ������ˮƽ���ϲ���������
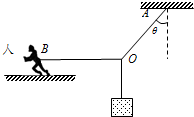
��ͼ��ʾ�����ͨ��3���������ң�3�������Ľ��ΪO������OBˮƽ��B����վ��ˮƽ���ϵ�����Ϊm2=60kg��������������OA����ֱ����ļнǦ�=37�㣬��鼰�˶����ھ�ֹ״̬����֪����ˮƽ��֮��Ķ�Ħ������Ϊ��=0.3��sin37��=0.6��cos37��=0.8��ȡg=10m/s2�������Ħ�������ڻ���Ħ������Ҫ������ˮƽ���ϲ������������� ��1������������������֧�����;�Ħ����������Ħ�����ﵽ���ʱ�����������ƽ��������ʽ��⼴�ɣ�
��2�������m���������ʱ��OB���ӵ��������O���������������ݹ�����ƽ��������ʽ�����������m1���ֵ��
���  �⣺��1��������OB���ܵ��������ΪFBm���������֮������Ħ����Ϊfmax������ˮƽ���ϲ������������ƽ���������У�
�⣺��1��������OB���ܵ��������ΪFBm���������֮������Ħ����Ϊfmax������ˮƽ���ϲ������������ƽ���������У�
fmax=��m2g
FBm=fmax
��ã�
FBm=180N
��2����������m1���ʱΪm1m������ˮƽ���ϲ��������Խ��OΪ�о�����������OA��O���������ΪFA������OB��O���������ΪFB����
FB=FBm
FB=FAsin��
FAcos��=m1mg
��ã�
m1m=24kg
�𣺣�1������OB���ܵ���������ܳ���180N��
��2����������m1����ܳ���24kg��
���� �����漰������ƽ���м�ֵ���⣬�������Ҫ����ʱ�������ľ�Ħ�����ﵽ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 �й��ѳ�Ϊ�����ϸ���ϵͳ������ȫ������������ǿ����Ӫ�����������ٶ���ߡ��ڽ���ģ���Ĺ��ң������ƣ���һ�������г�ǣ�����ʴ�9000kW�����������ٶ�Ϊ350km/h������һ�������г���ȫ��Լ1300km�ľ����ߴӱ������Ϻ����ڶ����Ϻĵ�ԼΪ��������
�й��ѳ�Ϊ�����ϸ���ϵͳ������ȫ������������ǿ����Ӫ�����������ٶ���ߡ��ڽ���ģ���Ĺ��ң������ƣ���һ�������г�ǣ�����ʴ�9000kW�����������ٶ�Ϊ350km/h������һ�������г���ȫ��Լ1300km�ľ����ߴӱ������Ϻ����ڶ����Ϻĵ�ԼΪ��������| A�� | 3.3��104kW•h | B�� | 3.1��106kW•h | C�� | 1.8��104kW•h | D�� | 3.3��105kW•h |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
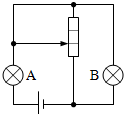 ��ͼ��ʾ��·�У���Դ���費�ɺ��ԣ�A��B���Ƶ���ֱ�ΪR��4R�������������Ļ�Ƭ�ƶ������µ���2��1��λ��ʱ���ƹ�����ͬΪP��������Ƭ�ƶ������϶ˣ�������
��ͼ��ʾ��·�У���Դ���費�ɺ��ԣ�A��B���Ƶ���ֱ�ΪR��4R�������������Ļ�Ƭ�ƶ������µ���2��1��λ��ʱ���ƹ�����ͬΪP��������Ƭ�ƶ������϶ˣ�������| A�� | A�Ʊ�����B�Ʊ䰵 | B�� | A�Ʊ䰵��B�Ʊ��� | ||
| C�� | ������������������Ϊ12R | D�� | A�ƹ��ʵ���$\frac{9}{16}$P |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 4 | C�� | 3 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 һͬѧҪ�о����ʵ��ɵĵ��������뵯�ɳ��ȸı����Ĺ�ϵ��ʵ�����£��������߶�Ϊh�Ĺ⻬ˮƽ�����ϣ����������ӱ�Ե��ֱ�ķ������һ���ʵ��ɣ�����˹̶����Ҷ�������Ϊm��һС����Ӵ���������һ�ش���������ϰ�ֽ�������ɴ�����Ȼ����ʱ��С����ǡ�������ӱ�Ե����ͼ��ʾ���ø�������ѹ������һ�ξ���x���ɾ�ֹ�ͷţ�ʹ������ˮƽ����������棬С���ڿ��з��к��䵽ˮƽ���棬ˮƽ����ΪS�����������ٶ�Ϊg��
һͬѧҪ�о����ʵ��ɵĵ��������뵯�ɳ��ȸı����Ĺ�ϵ��ʵ�����£��������߶�Ϊh�Ĺ⻬ˮƽ�����ϣ����������ӱ�Ե��ֱ�ķ������һ���ʵ��ɣ�����˹̶����Ҷ�������Ϊm��һС����Ӵ���������һ�ش���������ϰ�ֽ�������ɴ�����Ȼ����ʱ��С����ǡ�������ӱ�Ե����ͼ��ʾ���ø�������ѹ������һ�ξ���x���ɾ�ֹ�ͷţ�ʹ������ˮƽ����������棬С���ڿ��з��к��䵽ˮƽ���棬ˮƽ����ΪS�����������ٶ�Ϊg��| ���ɳ���ѹ����x��cm�� | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
| �������ˮƽ����S��m�� | 1.01 | 1.50 | 2.01 | 2.48 | 3.01 | 3.50 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ����Ե�����������������������ܵ����� | |
| B�� | ̫���Ե��������ʹ��������̫���˶� | |
| C�� | �������������ܵ�����������������ܵ���������������Dz�ͬ�� | |
| D�� | ֻ�������ܴ������֮���������������������С������֮�䲻������������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��L�ǵ��費�Ƶ��Ը���Ȧ��C�ǵ�������EΪ��Դ���ڿ���S�պϺͶϿ�ʱ�����ڵ������Ĵ������������˵����ȷ���ǣ�������
��ͼ��ʾ��L�ǵ��費�Ƶ��Ը���Ȧ��C�ǵ�������EΪ��Դ���ڿ���S�պϺͶϿ�ʱ�����ڵ������Ĵ������������˵����ȷ���ǣ�������| A�� | S�պ�˲�䣬A������磬B������� | |
| B�� | S���ֱպϣ�A������磬B������� | |
| C�� | S�Ͽ�˲�䣬A������磬B������� | |
| D�� | ������ȦL�ĵ��費�ƣ�����������·��������������µ������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ijͬѧ����ͼʾװ�ã���֤�����������ɣ�
ijͬѧ����ͼʾװ�ã���֤�����������ɣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
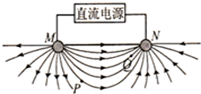 �ڵ����ϲ���һ�Ե缫M��N���������缫��ֱ����Դ������������γɺ㶨�����ͺ㶨�糡���㶨�糡�Ļ��������뾲�糡��ͬ����糡�߷ֲ���ͼ��P��Q�ǵ糡�е����㣮����˵����ȷ���ǣ�������
�ڵ����ϲ���һ�Ե缫M��N���������缫��ֱ����Դ������������γɺ㶨�����ͺ㶨�糡���㶨�糡�Ļ��������뾲�糡��ͬ����糡�߷ֲ���ͼ��P��Q�ǵ糡�е����㣮����˵����ȷ���ǣ�������| A�� | P�㳡ǿ��Q�㳡ǿС | |
| B�� | P����Ʊ�Q����Ƹ� | |
| C�� | P����ӵĵ����ܱ�Q����ӵĵ����ܴ� | |
| D�� | ������ֱ�ߴ�N��M�Ĺ��������ܵ糡���㶨���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com