
| 3 |

| v0 |
| cos60° |
| vy |
| 2 |
| v2 |
| R |
| mv |
| qB |
| 9×10-31×4×107 |
| 1.6×10-19×9×10-3 |
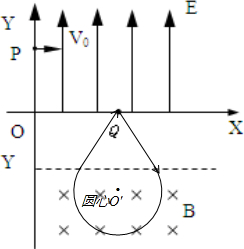
| r2+(Rcos30°)2 |
15+5
| ||
| 4 |
15+5
| ||
| 4 |
15+5
| ||
| 4 |


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中物理 来源:不详 题型:问答题
查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
| ||
| 3 |
| q |
| m |
查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
| 3 |
| R |
|
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:高中物理 来源:不详 题型:多选题
| A.能确定粒子通过y轴时的位置 |
| B.能确定粒子速度的大小 |
| C.能确定粒子在磁场中运动所经历的时间 |
| D.以上三个判断都不对 |

查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
| q |
| m |

查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题

查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
| q |
| m |
| π |
| 15 |
| 4π |
| 5 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com