
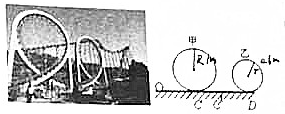
 过山车是人们喜爱的一项活动,某一游乐场过山车可简化为如图的模型:如图所示,甲、乙两个光滑的圆形轨道安置在同一竖直平面上,半径分别为R=1m和r=0.6m,在两轨道之间有一条长为L=3m水平轨道CD相通,一质量为1kg的小球以一定的速度先滑上甲轨道,通过CD段后又滑上乙轨道,最后从乙轨道最低点滑离轨道,小球运动过程中一直未脱离轨道,且小球与水平轨道间的动摩擦因数为μ=0.2,问:
过山车是人们喜爱的一项活动,某一游乐场过山车可简化为如图的模型:如图所示,甲、乙两个光滑的圆形轨道安置在同一竖直平面上,半径分别为R=1m和r=0.6m,在两轨道之间有一条长为L=3m水平轨道CD相通,一质量为1kg的小球以一定的速度先滑上甲轨道,通过CD段后又滑上乙轨道,最后从乙轨道最低点滑离轨道,小球运动过程中一直未脱离轨道,且小球与水平轨道间的动摩擦因数为μ=0.2,问:分析 (1)小球在两圆轨道的最高点对轨道的压力恰好为零,都由重力提供向心力,根据牛顿第二定律求出小球经过圆形轨道最高点时的速率.当小球从C到达甲圆形轨道的最高点的过程中,只有重力做功,根据机械能守恒定律求解小球刚进入甲轨道时的速度v0.
(2)根据动能定理求小球经过乙轨道最低点时的速度,再由牛顿定律求小球对轨道的压力.
解答 解:(1)设小球恰好通过甲轨道最高点的速度为v1,则有
mg=m$\frac{{v}_{1}^{2}}{R}$
解得 v1=$\sqrt{gR}$
取轨道最低点所在水平面为参考平面,从C到甲轨道的最高点的塩,由机械能守恒定律有
$\frac{1}{2}$mv012=mg•2R+$\frac{1}{2}$mv12
解得 v01=$\sqrt{5gR}$=$\sqrt{5×10×1}$=5$\sqrt{2}$m/s
小球恰好通过乙轨道最高点时的速度 v2=$\sqrt{gr}$=$\sqrt{6}$m/s
从C到乙轨道最高点的过程,由动能定理得
-mg•2r=-μmgL=$\frac{1}{2}$mv22-$\frac{1}{2}$mv022,解得 v02=$\sqrt{42}$m/s<v01
所以小球刚进入甲轨道时的速度v0至少为5$\sqrt{2}$m/s.
(2)若小球以(1)问中的最小速度进入甲轨道,设小球经过乙轨道最低点时速度为vD.
从C运动到D的过程,由动能定理得
-μmgL=$\frac{1}{2}$mvD2-$\frac{1}{2}$mv012.
在D点,由牛顿第二定律得
F′-mg=m$\frac{{v}_{D}^{2}}{r}$
联立可得 F′=$\frac{220}{3}$N
根据牛顿第三定律知,小球经过乙轨道最低点时对轨道的压力 F=F′=$\frac{220}{3}$N
答:
(1)小球刚进入甲轨道时的速度v0至少为5$\sqrt{2}$m/s.
(2)小球经过乙轨道最低点时对轨道的压力F为$\frac{220}{3}$N.
点评 本题是向心力、机械能守恒定律、动能定理的综合应用.在竖直平面内,小球沿光滑圆轨道的运动模型与轻绳拴的球的运动模型相似,最高点的速度是v=$\sqrt{gr}$.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中物理 来源: 题型:选择题
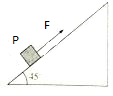 如图所示,位于固定的倾角为θ=45°粗糙斜面上的小物块P,受到一沿斜面向上的拉力F,沿斜面匀速上滑.现把力F的方向变为竖直向上而大小不变,仍能使物块P沿斜面保持原来的速度匀速运动,则物块与斜面间的动摩擦因数为( )
如图所示,位于固定的倾角为θ=45°粗糙斜面上的小物块P,受到一沿斜面向上的拉力F,沿斜面匀速上滑.现把力F的方向变为竖直向上而大小不变,仍能使物块P沿斜面保持原来的速度匀速运动,则物块与斜面间的动摩擦因数为( )| A. | μ=$\frac{\sqrt{2}}{2}$ | B. | μ=$\sqrt{2}$ | C. | μ=$\sqrt{2}$-1 | D. | μ=$\sqrt{2}$+1 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 核反应原理是氢的原子核在装置中聚变成氦粒,同时释放出大量的能量,和太阳发光的原理类似 | |
| B. | 线圈的作用是通电产生磁场使氘核等带电粒子在磁场中旋转而不溢出 | |
| C. | 这种装置同我国秦山、大亚湾核电站所使用核装置核反应原理相同 | |
| D. | 这种装置可以控制热核反应速度,使聚变能缓慢而稳定的释放 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
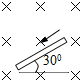 如图所示,长为20cm的直导线中的电流强度为2A,匀强磁场的磁感应强度为0.5T,磁场方向垂直纸面向里,则导线所受的安培力大小为0.2N.
如图所示,长为20cm的直导线中的电流强度为2A,匀强磁场的磁感应强度为0.5T,磁场方向垂直纸面向里,则导线所受的安培力大小为0.2N.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | φ=$\frac{{E}_{p}}{q}$ | B. | φ=$\frac{2{E}_{p}}{q}$ | C. | φ=$\frac{2{E}_{p}}{3q}$ | D. | φ=$\frac{{E}_{p}}{2q}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
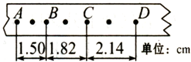 某同学在研究小车运动实验中,获得一条点迹清晰的纸带.每隔0.02s打一个点,该同学选择A、B、C、D四个计数点,测量数据如图所示,单位是cm.(结果均保留三位有效数字)
某同学在研究小车运动实验中,获得一条点迹清晰的纸带.每隔0.02s打一个点,该同学选择A、B、C、D四个计数点,测量数据如图所示,单位是cm.(结果均保留三位有效数字)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 由R=$\frac{U}{I}$知,导体的电阻由两端的电压和通过的电流决定 | |
| B. | 导体的电阻由导体本身的性质决定,跟导体两端的电压及流过导体的电流的大小无关 | |
| C. | 对于确定的导体,其两端的电压和流过它的电流的比值等于它的电阻值 | |
| D. | 电流相同时,电阻越大,其电压降越大 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
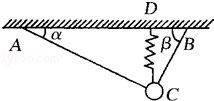 如图所示,一小物体重G=100N,用细线AC、BC和竖直的轻弹簧吊起,处于平衡状态.弹簧原长L0=1.5cm,劲度系数k=8000N/m,细线AC长s=4cm,α=30°,β=60°,求细线AC对小物体拉力的大小.
如图所示,一小物体重G=100N,用细线AC、BC和竖直的轻弹簧吊起,处于平衡状态.弹簧原长L0=1.5cm,劲度系数k=8000N/m,细线AC长s=4cm,α=30°,β=60°,求细线AC对小物体拉力的大小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com