
 如图,有理想边界的正方形匀强磁场区域abcd边长为L,磁场方向垂直纸面向里,磁感应强度大小为B.一群质量为m、带电量为+q的粒子(不计重力),在纸面内从b点沿各个方向以大小为$\frac{2qBL}{m}$的速率射入磁场,不考虑粒子间的相互作用,下列判断正确的是( )
如图,有理想边界的正方形匀强磁场区域abcd边长为L,磁场方向垂直纸面向里,磁感应强度大小为B.一群质量为m、带电量为+q的粒子(不计重力),在纸面内从b点沿各个方向以大小为$\frac{2qBL}{m}$的速率射入磁场,不考虑粒子间的相互作用,下列判断正确的是( )| A. | 从a点射出的粒子在磁场中运动的时间最短 | |
| B. | 从d点射出的粒子在磁场中运动的时间最长 | |
| C. | 从cd边射出的粒子与c的最小距离为($\sqrt{3}$-1)L | |
| D. | 从cd边射出的粒子在磁场中运动的最短时间为$\frac{πm}{6qB}$ |
分析 分析可知粒子半径均为2L,当粒子轨迹圆弧所对弦最短的时候,粒子在磁场中运动的时间最短;反之弦最长的时候,粒子在磁场中运动的时间最长;找到从cd边射出的粒子与c的最小距离的情况,画出粒子运动过程图,根据洛伦兹力提供向心力,得到半径公式R=$\frac{mv}{qB}$,结合几何关系,联立即可求解最小距离;找出从cd边射出的粒子在磁场中运动时间最短的情况,画出粒子轨迹过程图,利用周期公式T=$\frac{2πm}{qB}$结合所转过的圆心角,即可求解粒子在磁场中运动的最小时间.
解答 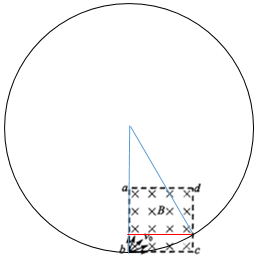 解:A、b点发射初速度指向a时的粒子在磁场中运动的时间最短,该粒子从b点射出,其时间最短为0,故A错误;
解:A、b点发射初速度指向a时的粒子在磁场中运动的时间最短,该粒子从b点射出,其时间最短为0,故A错误;
B、因为各个方向的粒子运动半径均相同:R=$\frac{mv}{qB}$=2L,周期也均相同:T=$\frac{2πm}{qB}$,当粒子在磁场中运动的轨迹圆弧所对的弦越长,其圆心角也越大,根据t=$\frac{θ}{2π}$T,可知时间越长,分析可知最长的弦即为bd的连线,所以从d点射出的粒子在磁场中运动的时间最长,故B正确;
C、如图所示,沿bc方向发射的粒子,从cd点射出时与c的最小距离△x最小,根据几何关系可得:(2L-△x)2+L2=(2L)2,解得:△x=(2-$\sqrt{3}$)L,故C错误;
D、分析可知,从cd边射出的粒子中,沿bc方向发射的粒子在磁场中运动的时间最短,根据周期公式T=$\frac{2πm}{qB}$,粒子转过的圆心角为30°,可求该粒子在磁场中运动的时间为t=$\frac{30°}{360°}T$=$\frac{πm}{6qB}$,故D正确;
故选:BD
点评 本题考查带电粒子在磁场中的匀速圆周运动,解题的关键是找到临界条件,画出粒子轨迹过程图,洛伦兹力提供向心力求出半径公式,结合几何关系.


科目:高中物理 来源: 题型:选择题
| A. | 物体每个分子无规则运动的动能都增大 | |
| B. | 物体分子无规则运动的平均动能增大 | |
| C. | 物体一定从外吸热 | |
| D. | 物体运动的动能一定增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 若加速度与速度方向相同,虽然加速度减小,物体的速度还是增大的 | |
| B. | 若加速度与速度方向相反,虽然加速度增大,物体的速度还是减小的 | |
| C. | 不管加速度与速度方向关系怎样,加速度增大时物体的速度一定增大 | |
| D. | 因为物体做匀变速直线运动,故其加速度是均匀变化的 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
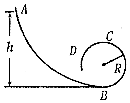 在竖直面内,光滑的曲线轨道ABCD,轨道最低点B处的切线沿水平方向,BCD部分是半径R=0.4m的圆形轨道,C点是圆形轨道的最高点,如图所示,现有一质量m=0.10kg的钢球(可视为质点),从轨道AB段上的某点由静止开始滑下,已知重力加速度g=10m/s2,空气阻力忽略不计.求:
在竖直面内,光滑的曲线轨道ABCD,轨道最低点B处的切线沿水平方向,BCD部分是半径R=0.4m的圆形轨道,C点是圆形轨道的最高点,如图所示,现有一质量m=0.10kg的钢球(可视为质点),从轨道AB段上的某点由静止开始滑下,已知重力加速度g=10m/s2,空气阻力忽略不计.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 2倍 | B. | $\frac{1}{2}$倍 | C. | 4倍 | D. | $\frac{1}{4}$倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 90N | B. | 210N | C. | 340N | D. | 300N |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 伽利略发一了行星的运动规律,开普勒发现了万有引力定律 | |
| B. | 哥白尼创立地心说,“地心说”是错误的,“日心说”是对的,太阳是宇宙的中心 | |
| C. | 牛顿首次在实验室里较准确地测出了万有引力常量 | |
| D. | 牛顿将行星与太阳、地球与月球、地球与地面物体之间的引力规律推广到宇宙中的一切物体,提出了万有引力定律 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 1:16 | B. | 64:1 | C. | 16:1 | D. | 1:64 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com