
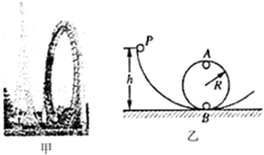
 游乐场的过山车可以底朝上的圆轨道上运行,游客却不会掉下来(如图甲).我们可以把它抽象成图乙所示的由曲面轨道和圆轨道平滑连接的模型(不计摩擦和空气阻力).若质量为m的小球从曲而轨道上的P点由静止开始下滑,并且可以顺利通过半径为R的圆轨道的最高点A.已知P点与B点的高度差h=3R.求:
游乐场的过山车可以底朝上的圆轨道上运行,游客却不会掉下来(如图甲).我们可以把它抽象成图乙所示的由曲面轨道和圆轨道平滑连接的模型(不计摩擦和空气阻力).若质量为m的小球从曲而轨道上的P点由静止开始下滑,并且可以顺利通过半径为R的圆轨道的最高点A.已知P点与B点的高度差h=3R.求:分析 (1)欲求B点的速度,只需对于P到B过程应用动能定理或者是机械能守恒都可以;
(2)先以小球为研究对象,利用牛顿第二定律求出轨道对小球的弹力,由牛顿第三定律知道小球对轨道的压力;
(3)首先求出刚好能通过最高点A点时的临界速度,再应用动能定理就可以了.
解答 解:(1)设小球在最低点的速度为V,由动能定理得:mgh=$\frac{1}{2}m{v}^{2}$
得:v=$\sqrt{2gh}$=$\sqrt{6gR}$
(2)取小球为研究对象,小球在A点的速度为VA,设轨道对小球的弹力为F,
由动能定理得:mg(h-2R)=$\frac{1}{2}m{v}_{A}^{2}$
由向心力定义和牛顿第二定律得:F+mg=$\frac{m{v}_{A}^{2}}{r}$
联立得:F=mg
由牛顿第三定律得:小球对轨道的压力为:F′=mg
(3)设小球刚好在A点的速度为V0,由向心力定义和牛顿第二定律得:
mg=$\frac{m{v}_{0}^{2}}{R}$
即:v0=$\sqrt{gR}$
设小球从P点运动到A点的过程中克服摩擦和空气阻力所做的功W,由动能定理得:
mg(h-2R)+W=$\frac{1}{2}m{v}_{0}^{2}$
得:W=-0.5mgR
所以小球克服阻力做功0.5mgR
答:(1)小球通过最低点B时速度$\sqrt{6gR}$;
(2)小球通过A点时对圆轨道的压力mg;
(3)小球从P点运动到A点的过程中克服摩擦和空气阻力所做的功为0.5mgR
点评 本题考查动能定理和圆周运动中向心力的分析,第二问中极容易漏掉牛顿第三定律的应用,
第三问中小球在A点的临界速度是关键.这是一道综合性较强的好题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中物理 来源: 题型:选择题
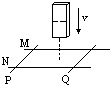 如图所示,光滑导轨MN水平放置,两根导体棒平行放于导轨上,形成一个闭合回路,当一条形磁铁从上方下落(未达导轨平面)的过程中,导体P、Q的运动情况是( )
如图所示,光滑导轨MN水平放置,两根导体棒平行放于导轨上,形成一个闭合回路,当一条形磁铁从上方下落(未达导轨平面)的过程中,导体P、Q的运动情况是( )| A. | P、Q互相靠扰 | B. | P、Q互相远离 | C. | P、Q均静止 | D. | 无法确定 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 重力对物体做功20J | B. | 人对物体做功20J | ||
| C. | 物体的机械能增加1.0J | D. | 合外力对物体做功1.0J |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
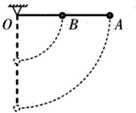 如图所示,一长为L的轻质细杆可绕其一端O点的竖直平面内自由转动,在杆的中点和另一端分别固定两个质量均为m的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,从开始运动到杆刚好转动到竖直位置的过程中,下列说法正确的是( )
如图所示,一长为L的轻质细杆可绕其一端O点的竖直平面内自由转动,在杆的中点和另一端分别固定两个质量均为m的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,从开始运动到杆刚好转动到竖直位置的过程中,下列说法正确的是( )| A. | B球机械能守恒 | |
| B. | A球运动到最低点时,重力的功率为2mg$\sqrt{\frac{3gL}{5}}$ | |
| C. | B球到达最低点时的速度为$\sqrt{\frac{3gL}{5}}$ | |
| D. | 细杆对A球做功为$\frac{1}{5}$mgL |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 人造地球卫星绕地球的运动可看成匀速圆周运动,它们做匀速圆周运动的线速度会随着轨道半径的变化而变化,现测得不同人造地球卫星的线速度V与轨道半径r的关系如图所示,已知引力常量为G,则可求得地球质量为( )
人造地球卫星绕地球的运动可看成匀速圆周运动,它们做匀速圆周运动的线速度会随着轨道半径的变化而变化,现测得不同人造地球卫星的线速度V与轨道半径r的关系如图所示,已知引力常量为G,则可求得地球质量为( )| A. | $\frac{Ga}{b}$ | B. | $\frac{Gb}{a}$ | C. | $\frac{a}{Gb}$ | D. | $\frac{b}{Ga}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 公式只适用于轨道是椭圆的运动 | |
| B. | 公式中的T为天体的自转周期 | |
| C. | 公式中的k值,只与中心天体有关,与绕中心天体公转的行星(或卫星)无关 | |
| D. | 若已知月球与地球之间的距离,根据开普勒第三定律公式可求出地球与太阳之间的距离 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
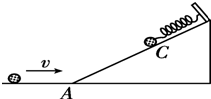 如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设小球在斜面最低点A的速度为V,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中弹簧弹性势能的增加量是( )
如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设小球在斜面最低点A的速度为V,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中弹簧弹性势能的增加量是( )| A. | mgh-$\frac{1}{2}$mv2 | B. | $\frac{1}{2}$mv2-mgh | C. | -mgh | D. | -[mgh+$\frac{1}{2}$mv2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com