

���� ��1����������Բ���˶������ڱ�������ٵ�ѹ��������ͬ��⼴�ɣ�
��2���������������ṩ��������⼴�ɣ�
��3������������ӵ��������˶���������ʱ�䣬�������ʱ��
��� �⣺��1����������ǿ�ų�����Բ���˶�������Ϊ��T=$\frac{2��m}{qB}$
Ҫ��֤t1=0ʱ�̲���������ÿ��ͨ������ʱ���ܱ����٣�������Բ���˶������ڱ�������ٵ�ѹ��������ͬ������������$\frac{2��m}{qB}$=$\frac{1}{f}$
��� B=$\frac{2��mf}{q}$
��2���� t1=0ʱ�̲��������ӵ�1�ξ����������ٶ�Ϊv1���뾶Ϊr1
qU0=$\frac{1}{2}$mv12
qv1B=m$\frac{{v}_{1}^{2}}{{r}_{1}}$
��ã�r1=$\frac{1}{B}$$\sqrt{\frac{2m{U}_{0}}{q}}$
ͬ�������ӵ�2�ξ��������İ뾶r2=$\frac{1}{B}$$\sqrt{\frac{2m•2{U}_{0}}{q}}$
��r1��r2=1��$\sqrt{2}$
��3�������ӵ������ʱ���ٶ�Ϊvm����
qvmB=m$\frac{{v}_{m}^{2}}{R}$
�����дӳ��ڷɳ������ӣ��ٶȶ���ͬ����ÿһ������ʱ����ÿ�������ڴų��У����糡�������Σ���ij�����ӱ�����ʱ�ĵ�ѹΪU�����ܹ���������n�Σ���
nqU=$\frac{1}{2}m{v}_{m}^{2}$
������ n=$\frac{2{��}^{2}m{f}^{2}{R}^{2}}{qU}$
�����ڴų����˶�����ʱ��t=$n•\frac{T}{2}$
������ t=$\frac{{��}^{2}mf{R}^{2}}{qU}$
t2=$\frac{1}{6f}$ʱ�̲��������ӱ�����ʱ�ĵ�ѹΪU2=U0cos��2��f$•\frac{1}{6}f$��=$\frac{{U}_{0}}{2}$
���ԣ�t1=0��t2=$\frac{1}{6f}$ʱ�̲��������ӵ�����ڴ���ʱ���Ϊ��t=$\frac{1}{6f}$+$\frac{{��}^{2}mf{R}^{2}}{q\frac{{U}_{0}}{2}}$-$\frac{{��}^{2}mf{R}^{2}}{q{U}_{0}}$
����t=$\frac{1}{6f}$+$\frac{{��}^{2}mf{R}^{2}}{q{U}_{0}}$
��1���Ÿ�Ӧǿ��B�Ĵ�С $\frac{2��mf}{q}$��
��2��t1=0ʱ�̲��������ӵ�1�κ͵�2�ξ�����D�κм���������뾶֮��1��$\sqrt{2}$��
��3��t1=0��t2=$\frac{1}{6f}$ʱ�̲��������ӵ�����ڴ���ʱ����$\frac{1}{6f}$+$\frac{{��}^{2}mf{R}^{2}}{q{U}_{0}}$��
���� �����ѶȽϴ��ر��ǵ�3�ʣ��Ȿ��Ĺؼ���֪�������������Ĺ���ԭ�������Ӧ�����������ṩ��������⣬��Ҫע�������̵ļ�������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ˮƽ���ϵĶ����ʵ�С���壬���ΪL����������ȣ���������ͬ�ij��ٶȴ�ͼʾλ�ÿ�ʼ������ͬһֱ���˶������������ֹͣ�˶�ʱ�ľ���Ϊs��������
ˮƽ���ϵĶ����ʵ�С���壬���ΪL����������ȣ���������ͬ�ij��ٶȴ�ͼʾλ�ÿ�ʼ������ͬһֱ���˶������������ֹͣ�˶�ʱ�ľ���Ϊs��������| A�� | ����ͼ��B������ǹ⻬�ġ��Ҳ���������Ķ�Ħ��������ͬ����s��L | |
| B�� | ����ͼ��B������ǹ⻬�ġ��Ҳ���������Ķ�Ħ��������ͬ����s=L | |
| C�� | ������ˮƽ�涼�Ǿ��ȴֲڵġ�����������Ķ�Ħ��������ͬ����s��L | |
| D�� | ������ˮƽ�涼�Ǿ��ȴֲڵġ�����������Ķ�Ħ��������ͬ����s=L |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ���������������ɸ��¡���ѹ�ĵȵ������������������ɣ������������ϵ����ٶ�v0����P1��P2���������ǿ�ų��У�ƽ�е���ab��cd���������Ϊ��0s��1s�ڻ����ų⣬1s��3s�ڻ���������3s��4s�ڻ����ų⣮�涨��ȦA������Ϊ�Ÿ�Ӧǿ��B����������ô����ȦA�ڴŸ�Ӧǿ��B��ʱ��t�仯��ͼ������ǣ�������
��ͼ��ʾ���������������ɸ��¡���ѹ�ĵȵ������������������ɣ������������ϵ����ٶ�v0����P1��P2���������ǿ�ų��У�ƽ�е���ab��cd���������Ϊ��0s��1s�ڻ����ų⣬1s��3s�ڻ���������3s��4s�ڻ����ų⣮�涨��ȦA������Ϊ�Ÿ�Ӧǿ��B����������ô����ȦA�ڴŸ�Ӧǿ��B��ʱ��t�仯��ͼ������ǣ�������| A�� |  | B�� |  | C�� |  | D�� | 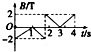 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ������ΪM��б���徲ֹ�ڴֲڵ�ˮƽ���ϣ�����Ϊm�Ļ�����M�Ĵֲ�б��AB�ȼ����»���������M��Ħ�����ķ���Ϊ��������
��ͼ��ʾ������ΪM��б���徲ֹ�ڴֲڵ�ˮƽ���ϣ�����Ϊm�Ļ�����M�Ĵֲ�б��AB�ȼ����»���������M��Ħ�����ķ���Ϊ��������| A�� | ˮƽ���� | B�� | ˮƽ���� | ||
| C�� | ˮƽ���һ�ˮƽ���� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ����λͬѧ������ҡ�����硱ʵ�飺��һ�������ߵ���������һ�����������Ƶ������������ϣ��γɱպϻ�·������ͬѧ����ҡ��AB��Ρ�����������ͼ���龰�����ڳ���������شų����������ƽ�У�����ָ��ͼ��ҡ������ͬѧ���ض���վ���ģ���ͬѧվ�����ߣ����յ��ߵ�A�㣻��ͬѧվ�ڶ��ߣ����յ��ߵ�B�㣮������˵����ȷ���ǣ�������
��ͼ��ʾ����λͬѧ������ҡ�����硱ʵ�飺��һ�������ߵ���������һ�����������Ƶ������������ϣ��γɱպϻ�·������ͬѧ����ҡ��AB��Ρ�����������ͼ���龰�����ڳ���������شų����������ƽ�У�����ָ��ͼ��ҡ������ͬѧ���ض���վ���ģ���ͬѧվ�����ߣ����յ��ߵ�A�㣻��ͬѧվ�ڶ��ߣ����յ��ߵ�B�㣮������˵����ȷ���ǣ�������| A�� | ��������ҡ����ߵ�ʱ���������е������ | |
| B�� | ��������ҡ��ˮƽλ��ʱ���������е������ | |
| C�� | ��������ҡ����͵�ʱ���������ܵ��İ�������� | |
| D�� | �������������˶�ʱ���������е�����A����B |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��CD�����ڳ�ǿ��СE=$\frac{mg}{q}$������ˮƽ�������ǿ�糡��һ������Ϊm�������Ϊ+q�Ĺ⻬��ԵС�ӵױ�BC��ΪL�����53��Ĺ⻬ֱ��������б�涥��A���ɾ�ֹ��ʼ�»����˶���б���C������һ�⻬��ֱ��Բ��ϸԲ���ڣ�C��ΪһС�γ��ȿɺ��ԵĹ⻬Բ����Բ���ھ��Դ���С��ֱ������Բֱ��CD����ֱ���ϣ���ǡ�ܵ���ϸԲ����ߵ�D�㣬����D���뿪�����б����ij��P�����������ٶ�Ϊg��sin53��=0.8��Cos53��=0.6����
��ͼ��ʾ��CD�����ڳ�ǿ��СE=$\frac{mg}{q}$������ˮƽ�������ǿ�糡��һ������Ϊm�������Ϊ+q�Ĺ⻬��ԵС�ӵױ�BC��ΪL�����53��Ĺ⻬ֱ��������б�涥��A���ɾ�ֹ��ʼ�»����˶���б���C������һ�⻬��ֱ��Բ��ϸԲ���ڣ�C��ΪһС�γ��ȿɺ��ԵĹ⻬Բ����Բ���ھ��Դ���С��ֱ������Բֱ��CD����ֱ���ϣ���ǡ�ܵ���ϸԲ����ߵ�D�㣬����D���뿪�����б����ij��P�����������ٶ�Ϊg��sin53��=0.8��Cos53��=0.6�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ����ɴ��ھ��������ڵ���뾶�ĸ߶��Ƶ�����Բ���˶�ʱ�����ڵ����ڵ����⣨����Ϊ��ƽ�й⣩���ڷɴ����еĹ����У���һ��ʱ��ɴ�����������Ӱ������ͼ��ʾ����֪����İ뾶ΪR����������ΪM����������ΪG�����ڷɴ��˶���һ�������ڣ��ɴ���̫���ܵ�ذ���ղ���̫�����ʱ��Ϊ��������
����ɴ��ھ��������ڵ���뾶�ĸ߶��Ƶ�����Բ���˶�ʱ�����ڵ����ڵ����⣨����Ϊ��ƽ�й⣩���ڷɴ����еĹ����У���һ��ʱ��ɴ�����������Ӱ������ͼ��ʾ����֪����İ뾶ΪR����������ΪM����������ΪG�����ڷɴ��˶���һ�������ڣ��ɴ���̫���ܵ�ذ���ղ���̫�����ʱ��Ϊ��������| A�� | T=$\frac{2��}{3}$$\sqrt{\frac{2{R}^{3}}{GM}}$ | B�� | T=$\frac{4��}{3}$$\sqrt{\frac{2{R}^{3}}{GM}}$ | C�� | T=��$\sqrt{\frac{2{R}^{3}}{GM}}$ | D�� | T=��$\sqrt{\frac{{R}^{3}}{GM}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ���������б�������»�����������»������зֱ�����ʩ��һ����ֱ���µĺ���F1��һ����б��ƽ�������·��ĺ���F2�����������б�����ֹ������������˵����ȷ���ǣ�������
��ͼ��ʾ���������б�������»�����������»������зֱ�����ʩ��һ����ֱ���µĺ���F1��һ����б��ƽ�������·��ĺ���F2�����������б�����ֹ������������˵����ȷ���ǣ�������| A�� | ����F1ʱ���������б�������»� | |
| B�� | ����F2ʱ���������б�������»� | |
| C�� | ����F1ʱ��б�治�ܵ����Ħ���� | |
| D�� | ����F2ʱ��б���ܵ������ҵ�Ħ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ�����ӴӾ�ֹ��ʼ����ѹΪU1�ĵ糡���ٺ���ˮƽ�ٶ�����ˮƽ���õ���ƽ�н������м䣮�������峤Ϊl���������ľ���Ϊd����ֱ���õ�ӫ���������������Ҷ˵ľ���ΪL�������������������ϵ�ѹU2ʱ�����ƫ�����ߴ���ӫ�����ϵ�P�㣮��֪���ӵĵ����Ϊe������Ϊm�����������Ϳ���������Ӱ�죮��
��ͼ��ʾ��һ�����ӴӾ�ֹ��ʼ����ѹΪU1�ĵ糡���ٺ���ˮƽ�ٶ�����ˮƽ���õ���ƽ�н������м䣮�������峤Ϊl���������ľ���Ϊd����ֱ���õ�ӫ���������������Ҷ˵ľ���ΪL�������������������ϵ�ѹU2ʱ�����ƫ�����ߴ���ӫ�����ϵ�P�㣮��֪���ӵĵ����Ϊe������Ϊm�����������Ϳ���������Ӱ�죮���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com