
| A. | 该彗星公转的周期小于火星的公转周期 | |
| B. | 该彗星公转的线速度大于木星公转的线速度 | |
| C. | 该彗星的向心加速度大于火星的向心加速度 | |
| D. | 人类发射探测器登陆该彗星,发射速度必须大于11.2km/s |
分析 根据万有引力提供向心力GMmr2=mv2r=m\frac{4{π}^{2}}{{T}^{2}}r=ma,解出线速度、周期、向心加速度以及角速度与轨道半径大小的关系,再依据第一宇宙与第二宇宙速度的概念,从而即可求解.
解答 解:A、B、根据万有引力提供向心力G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}=m\frac{4{π}^{2}}{{T}^{2}}r=ma,
得v=\sqrt{\frac{GM}{r}},T=2π\sqrt{\frac{{r}^{3}}{GM}}.由此可知,轨道半径越大,线速度越小、周期越大,由于火星到太阳的距离小于彗星到太阳的距离,所以v火>v彗,
T火<T彗.故AB错误.
C、据万有引力提供向心加速度,得:G\frac{Mm}{{r}^{2}}=ma,可知轨道半径比较小的火星的向心加速度比较大.故C错误;
D、要挣脱地球的束缚,发射速度必须大于11.2km/s.故D正确.
故选:D.
点评 本题考查万有引力定律的应用,要掌握万有引力提供向心力,并能够根据题意选择不同的向心力的表达式,注意第一宇宙速度与第二宇宙速度的区别.


科目:高中物理 来源: 题型:选择题
| A. | 月球表面的重力加速度g月=\frac{h{v}_{0}^{2}}{{L}^{2}} | |
| B. | 月球的平均密度ρ=\frac{3h{v}_{0}^{2}}{2πG{L}^{2}R} | |
| C. | 月球的第一宇宙速度v=\frac{{v}_{0}}{L}\sqrt{2h} | |
| D. | 月球的质量m月=\frac{h{R}^{2}{v}_{0}^{2}}{G{L}^{2}} |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
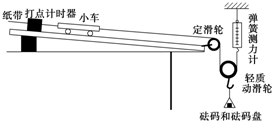

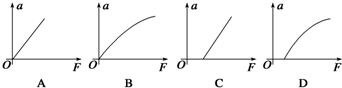
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
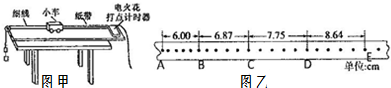
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
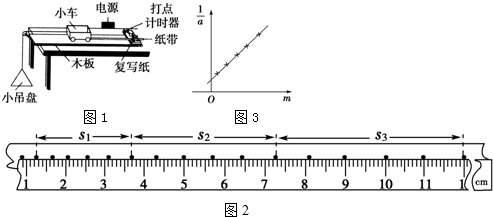
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
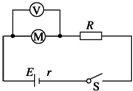 如图所示,一直流电动机与阻值R=9Ω的电阻串联在电源上,电源电动势E=30V,内阻r=1Ω,用理想电压表测出电动机两端电压U=10V,已知电动机线圈电阻RM=1Ω,则下列说法中正确的是( )
如图所示,一直流电动机与阻值R=9Ω的电阻串联在电源上,电源电动势E=30V,内阻r=1Ω,用理想电压表测出电动机两端电压U=10V,已知电动机线圈电阻RM=1Ω,则下列说法中正确的是( )| A. | 通过电动机的电流为10 A | B. | 通过电动机的电流小于10 A | ||
| C. | 电动机的输出功率小于16 W | D. | 电源的输出功率为56 W |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com