

���� ��1���������ܵ��糡������������ƽ��ʱ��������ֱ���˶�������ɵ�ѹ���Ÿ�Ӧǿ�ȿ�����˶��ٶȣ�
��2�������ڵ糡������ƽ���˶������˶��ֽ���ص糡ǿ�ȷ����봹ֱ�糡ǿ�ȷ���Ȼ�����˶�ѧ��ʽ��⣮�����뿪�糡��������ֱ���˶����Ӷ��������ƫת����ı���ʽ�����͵õ����ӵĺ��ʱȱ���ʽ��
��3�������˶�ѧ��ʽ�����ţ�ٵڶ����ɣ������ι�ϵ��������⣻
��4������ʵ��ķ�����ȷ������ӱȺɵķ�����
���  �⣺��1�������ڼ���M��N��糡�������������������������������˶�������ƽ�⣬����ӽ��뼫�����ٶ�Ϊv����ƽ�������� evB=eE
�⣺��1�������ڼ���M��N��糡�������������������������������˶�������ƽ�⣬����ӽ��뼫�����ٶ�Ϊv����ƽ�������� evB=eE
�������糡ǿ�� $E=\frac{U}{d}$
��� $v=\frac{U}{Bd}$
��2������M��N�������ǿ�ų�ʱ���������뾶Ϊr������Բ���˶�������ų������������ֱ���˶�����ͼ��ʾ$tan��=\frac{L_1}{{\sqrt{{r^2}-L_1^2}}}$
�����ų�������ֱ�������ƶ��ľ���${y_3}={L_2}tan��=\frac{{{L_1}{L_2}}}{{\sqrt{{r^2}-L_1^2}}}$
$y=r-\sqrt{{r^2}-L_1^2}+{y_3}$
���$y=r-\sqrt{{r^2}-L_1^2}+\frac{{{L_1}{L_2}}}{{\sqrt{{r^2}-L_1^2}}}$
��3�������ڴų���������Բ���˶��İ뾶Ϊr�����������ṩ������$evB=m\frac{v^2}{r}$
��� $\frac{e}{m}=\frac{U}{{{B^2}dr}}$
��4������1�������Ե��Ӵ�����K�����ij��ٶȣ�����������̽������O��A֮��ļ����˶���̽�����е�����ֱ���˶�������������ӵıȺɣ������O��A��ļ��ٵ�ѹ
����2������������̽���ڡ����е��˶�������������ӵıȺɣ������P��P1֮��ľ���
�𣺣�1��������M��N��������ֱ���˶�ʱ���ٶȴ�СΪ$\frac{U}{Bd}$��
��2��������M��N��������Բ���˶��Ĺ켣�뾶r��L1��L2��y֮��Ĺ�ϵʽΪ$y=r-\sqrt{{r^2}-L_1^2}+\frac{{{L_1}{L_2}}}{{\sqrt{{r^2}-L_1^2}}}$
��3������֪������M��N��������Բ���˶��Ĺ켣�뾶r�����ӵıȺ�Ϊ$\frac{e}{m}=\frac{U}{{{B^2}dr}}$
��4������1�������Ե��Ӵ�����K�����ij��ٶȣ�����������̽������O��A֮��ļ����˶���̽�����е�����ֱ���˶�������������ӵıȺɣ������O��A��ļ��ٵ�ѹ
����2������������̽���ڡ����е��˶�������������ӵıȺɣ������P��P1֮��ľ���
���� ����Ϊ���������ڵ�ų��е��˶����ɣ�Ҫע����ȷ�糡�е���ƽ�ף��ų��е�Բ���˶��ķ������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
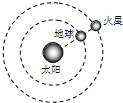 �о�����������̽������������һ����Ҫ���裮����Ǻ͵������̫��������Բ���˶������ǹ���ڵ�������࣬��ͼ��ʾ���������Ƚϣ�������˵������ȷ���ǣ�������
�о�����������̽������������һ����Ҫ���裮����Ǻ͵������̫��������Բ���˶������ǹ���ڵ�������࣬��ͼ��ʾ���������Ƚϣ�������˵������ȷ���ǣ�������| A�� | ���������ٶȽϴ� | B�� | �������н��ٶȽϴ� | ||
| C�� | �����������ڽϴ� | D�� | �������е����ļ��ٶȽϴ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��һľ���Գ��ٶ�v0�ӵ˳������ϴֲڵ�б�棬�ٶȼ�Ϊ����ٷ��س����㣬��֪ȫ��������ʱΪT������ͼ���У�����ȷ��ʾľ������һ������������ʱ���ϵ���ǣ�������
��ͼ��һľ���Գ��ٶ�v0�ӵ˳������ϴֲڵ�б�棬�ٶȼ�Ϊ����ٷ��س����㣬��֪ȫ��������ʱΪT������ͼ���У�����ȷ��ʾľ������һ������������ʱ���ϵ���ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����������ŵ�ɵ���ƽ�н��������������ֱ���ã�M��NΪ���ͬһ�糡���ϵ����㣮һ�������ӣ��������������ٶ�vM����M���ص糡�������˶�����δ���Ҳ������Ӵ���һ��ʱ����������ٶ�vN����N�㣮������
��ͼ��ʾ����������ŵ�ɵ���ƽ�н��������������ֱ���ã�M��NΪ���ͬһ�糡���ϵ����㣮һ�������ӣ��������������ٶ�vM����M���ص糡�������˶�����δ���Ҳ������Ӵ���һ��ʱ����������ٶ�vN����N�㣮������| A�� | �糡��M��ĵ���һ������N��ĵ��� | |
| B�� | �����ܵ��糡��һ����Mָ��N�� | |
| C�� | ������M���ٶ�һ������N����ٶȴ� | |
| D�� | ������M�������һ������N��ĵ����ܴ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | �ʵ�P��ʱ�̵��ٶ���x��������� | |
| B�� | �ʵ�P��ʱ�̵ļ��ٶ���x��������� | |
| C�� | �ٹ��������ʱ���ʵ�P��λ��Ϊ��ֵ | |
| D�� | ����һ�����ڣ��ʵ�Pͨ����·��Ϊ2a |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
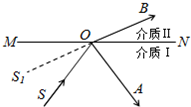 ��ͼ��ʾ��MN�ǽ��ʢ�ͽ��ʢ�Ľ����棬���ʢ��еĹ�ԴS������һ���������ڽ������O���ֳ�������OA��OB�������������O�������������SO˳ʱ����ת��S1O��λ�ã�������ת����������˵����ȷ���ǣ�������
��ͼ��ʾ��MN�ǽ��ʢ�ͽ��ʢ�Ľ����棬���ʢ��еĹ�ԴS������һ���������ڽ������O���ֳ�������OA��OB�������������O�������������SO˳ʱ����ת��S1O��λ�ã�������ת����������˵����ȷ���ǣ�������| A�� | ����OA��ʱ����ת������ | B�� | ����OB��ʱ����ת������ | ||
| C�� | ����OB�����ҿ�����ʧ | D�� | ���ʢ�����ǹ������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 45s | B�� | 160s | C�� | 165s | D�� | 75s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ������Ϊm����ΪL��ֱ����������Եϸ��������O��O�䣬��������ǿ�ų��У�������ͨ����x��������ĺ㶨����I����������ֱ����ļн�Ϊ�ȣ��ҵ��߱��־�ֹ����Ÿ�Ӧǿ�ȵ���Сֵ�ͷ���Ϊ��������
��ͼ��ʾ������Ϊm����ΪL��ֱ����������Եϸ��������O��O�䣬��������ǿ�ų��У�������ͨ����x��������ĺ㶨����I����������ֱ����ļн�Ϊ�ȣ��ҵ��߱��־�ֹ����Ÿ�Ӧǿ�ȵ���Сֵ�ͷ���Ϊ��������| A�� | $\frac{mg}{IL}$tan�ȣ�z������ | B�� | $\frac{mg}{IL}$��y������ | ||
| C�� | $\frac{mg}{IL}$tan�ȣ�z�Ḻ�� | D�� | $\frac{mg}{IL}$sin�ȣ����������� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com