
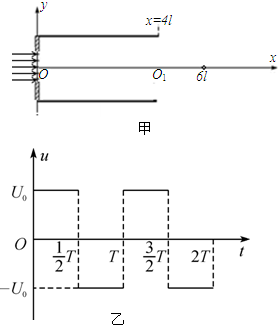
| 4l |
| nv0 |
| l |
| 2 |
| 1 |
| 2 |
| T |
| 2 |
| eU0 |
| 2lm |
nm
| ||
| 4e |
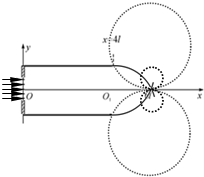
m
| ||
| rm |
| 2mv0 |
| 5el |
m
| ||
| rn |
| 2mv0 |
| el |
| T |
| 2 |
| T |
| 2 |
|
| 1 |
| 2 |
| T |
| 2 |
| 1 |
| 4 |
| nv0 |
| 2 |
| 1 |
| 2 |
| l |
| 2 |
| nv0t |
| 2 |
| (4k+3) |
| 2 |
| T |
| 2 |
|
| T |
| 2 |
| T |
| 2 |
| 1 |
| 2 |
| T |
| 2 |
| 1 |
| 2 |
| 4k+1 |
| 4 |
| 2l |
| n |
| 1 |
| 2 |
| 4k+1 |
| 2 |
| 1 |
| 2 |
| T |
| 2 |
| T |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| T |
| 2 |
| 4k+1 |
| 4 |
| 2l |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
| 4k+3 |
| 2 |
| 4l |
| nv0 |
nm
| ||
| 4e |
| 2mv0 |
| el |
| 2mv0 |
| 5el |
| (4k+1)l |
| 2 |
| nv0t |
| 2 |
| nv0t |
| 2 |
| (4k+3) |
| 2 |


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ������ ���ͣ���ѡ��
| A��һ�������� |
| B��һ���Ǵ��¶��ϴ���Ǧ�� |
| C�������Ǵ��϶��´���Ǧ�� |
| D�����ܴ����磬Ҳ���ܴ����� |

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ������ ���ͣ��ʴ���
| q |
| m |
| 3 |

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ������ ���ͣ��ʴ���

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ������ ���ͣ��ʴ���
| q |
| m |
| 3 |
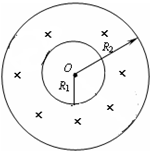
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ������ ���ͣ���ѡ��
| A��ʹa����Ƶ���b�壬�ų�����ֱֽ������ |
| B��ʹa����Ƹ���b�壬�ų�����ֱֽ������ |
| C��ʹa����Ƹ���b�壬�ų�����ֱֽ������ |
| D��ʹa����Ƶ���b�壬�ų�����ֱֽ������ |

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ������ ���ͣ���ѡ��
| A����С�ų��ĴŸ�Ӧǿ�� |
| B��������ǿ�糡��ļ��ٵ�ѹ |
| C������D�ν����еİ뾶 |
| D����С�����ľ��� |

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ������ ���ͣ���ѡ��
| A�������������ӵĵ��Ծ���ͬ���Ҿ������� | ||
| B�������������ӵĵ��Ծ���ͬ���Ҿ������� | ||
C�������������ӵ��ٶȾ���ͬ���Ҿ�Ϊ
| ||
D������a��b��������ӵ�����֮����m=
|

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ������ ���ͣ�������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com