
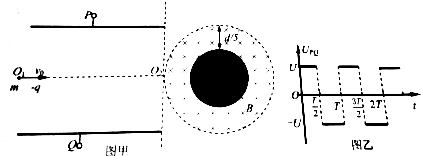
分析 (1)由于粒子在电场中的运动时间与电场的变化周期相等,所以粒子y方向先做匀加速运动,后做匀减速运动,加速度大小相同,所用时间相同,粒子离开电场时粒子恰好从下边水平缘射出进入磁场,由牛顿第二定律和运动学公式就能求出粒子在电场中偏离O1O2的最大距离,及该粒子离开电场区域时的速度.
(2)画出粒子在磁场中运动的轨迹,由几何关系求出粒子做匀速圆周运动的半径,由洛仑兹力提供向心力,求得磁感应强度B0.
(3)磁感应强度变为$\frac{1}{5}$B0,找到粒子恰好能打到圆柱体的临界几何条件,利用洛伦兹力提供向心力结合临界几何关系,即可求出粒子向下偏离O1O2的最远距离.
解答 解:(1)粒子通过两板时间:t=$\frac{L}{{v}_{0}}$=T
粒子在两板间运动加速度大小:a=$\frac{Eq}{m}$
E=$\frac{U}{d}$
第1个周期T内,由不同时刻进入电场的粒子,沿电场方向的速度vy随时间t变化的关系如图甲所示.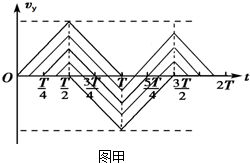
由图可知,t=n$\frac{T}{2}$(n取整数)时刻进入电场的粒子,在电场方向偏转的距离最大.
y=$2×\frac{1}{2}a(\frac{T}{2})^{2}$
解得:y=$\frac{d}{2}$
由图甲还可知,从不同时刻进入电场的粒子离开电场时竖直方向的速度均为0.
故离开电场时所有粒子的速度大小:v=v0,方向与初速度方向相同
(2)粒子以v=v0进入磁场,做匀速圆周运动,
根据洛伦兹力提供向心力:qv0B=m$\frac{{v}_{0}^{2}}{r}$
可得:r=$\frac{m{v}_{0}}{qB}$
由几何关系可知,粒子由磁场边界最高点相切射入时轨道半径最小,对应的磁场厚度最小.
即:2r=$\frac{d}{5}$
解得:B0=$\frac{10m{v}_{0}}{qd}$
(3)设粒子在磁场运动的半径为r1,根据洛伦兹力提供向心力可得:qv0$\frac{{B}_{0}}{5}$=m$\frac{{v}_{0}^{2}}{{r}_{1}}$
解得:r1=$\frac{5m{v}_{0}}{q{B}_{0}}$=$\frac{d}{2}$
由几何关系得:cosθ=$\frac{\frac{{r}_{1}+R}{2}}{{r}_{1}}$=0.8
y=(r1+R)cosθ-r1=$\frac{7}{50}$d=0.14d
y=0.14d为粒子射出电场瞬间偏离电场中轴线O1O2的距离,并非粒子在电场中运动偏离O1O2的最远距离.
考虑到粒子沿电场方向有往复运动情况,设在电场中向下偏离O1O2的最远距离为y1,粒子在偏离O1O2最远后再在垂直于O1O2方向往回走的位移为y2;
设这两段位移对应的时间分别为t1与t2,则:y1-y2=0.14d
由对称性可知:y1=$2×\frac{1}{2}a(\frac{{t}_{1}}{2})^{2}$,y2=$2×\frac{1}{2}a{(\frac{{t}_{2}}{2})}^{2}$
t1+t2=T
将a=$\frac{2d{v}_{0}^{2}}{{L}^{2}}$、T=$\frac{L}{{v}_{0}}$代入解得:y1=0.20d
答:(1)粒子在电场中偏离O1O2的最大距离为$\frac{d}{2}$,及该粒子离开电场区域时的速度为v0,方向与初速度方向相同;
(2)要使从电场中飞出的粒子恰好都不能打在圆柱体上,磁场的感应强度B0为$\frac{10m{v}_{0}}{qd}$;
(3)若磁感应强度变为$\frac{1}{5}$B0,此时能打到圆柱体上的粒子,其在电场中向下偏离O1O2的最远距离为0.20d.
点评 本题考查带电粒子在复合场中的运动,解题关键是要画出粒子轨迹过程图,选择合适的规律解决问题,粒子做类平抛运动时,运用运动的合成与分解法研究,在磁场中做匀速圆周运动时,利用洛伦兹力提供向心力求出半径公式结合几何关系解决,对数学平面几何要求较高.


科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
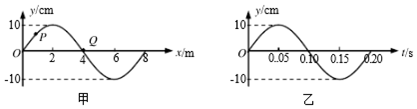
| A. | t=0.15s时,质点Q的加速度达到负向最大 | |
| B. | 从t=0.10s到t=0.25s,Q质点沿x轴负方向运动了6m | |
| C. | t=0.15s时,质点P的运动方向沿y轴负方向 | |
| D. | 从t=0.10s到t=0.25s,质点P通过的路程为30cm |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 氦离子(He+)从n=4能级跃迁到n=3能级比从n=3能级跃迁到n=2能级辐射出光子的频率低 | |
| B. | 大量处在n=3能级的氦离子(He+)向低能级跃迁,只能发出2种不同频率的光子 | |
| C. | 氦离子(He+)处于n=1能级时,能吸收45eV的能量跃迁到n=2能级 | |
| D. | 氦离子(He+)从n=3能级跃迁到n=2能级比从n=4能级跃迁到n=2能级辐射出的光容易衍射 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,质量m=2.0kg的物体静止在光滑水平面上,用F=8.0N的水平拉力,使物体由静止开始运动.求:
如图所示,质量m=2.0kg的物体静止在光滑水平面上,用F=8.0N的水平拉力,使物体由静止开始运动.求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
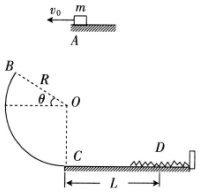 如图所示,半径R=0.4m的光滑圆弧轨道BC固定在竖直平面内,轨道的上端点B和圆心O的连 线与水平方向的夹角θ=30°,下端点C为轨道的最低点且与粗糙水平面相切,一根轻质弹簧的右端固定在 竖直挡板上.质量m=0.1kg的小物块(可视为质点)从空中的A点以v0=2m/s的速度被水平拋出,恰好从B点沿轨道切线方向进入轨道,经过C点后沿水平面向右运动至D点时,弹簧被压缩至最短,此时弹簧的弹性势能Epm=0.8J,已知小物块与水平面间的动摩擦因数μ=0.5,g取10m/s2.求:
如图所示,半径R=0.4m的光滑圆弧轨道BC固定在竖直平面内,轨道的上端点B和圆心O的连 线与水平方向的夹角θ=30°,下端点C为轨道的最低点且与粗糙水平面相切,一根轻质弹簧的右端固定在 竖直挡板上.质量m=0.1kg的小物块(可视为质点)从空中的A点以v0=2m/s的速度被水平拋出,恰好从B点沿轨道切线方向进入轨道,经过C点后沿水平面向右运动至D点时,弹簧被压缩至最短,此时弹簧的弹性势能Epm=0.8J,已知小物块与水平面间的动摩擦因数μ=0.5,g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
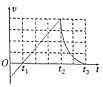 如图所示为某跳水运动员自离开跳板开始计时的速度与时间关系图象,假设空气阻力忽略不计,根据图象可知( )
如图所示为某跳水运动员自离开跳板开始计时的速度与时间关系图象,假设空气阻力忽略不计,根据图象可知( )| A. | t2时刻运动员到达起跳的最高点 | B. | t2~t3时间内,运动员处于失重状态 | ||
| C. | 0~t2时间内,运动员机械能守恒 | D. | 0~t3时间内,合力对运动员做负功 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 密立根通过油滴实验测出了基本电荷的数值 | |
| B. | 康普顿效应表明光子只具有能量,不具有动量 | |
| C. | 居里夫妇从沥青铀矿中分离出钋(Po)和镭(Ra)两种新元素 | |
| D. | 爱因斯坦在光电效应的基础上,提出了光子说 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com