
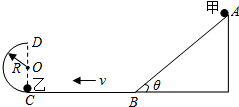
 如图所示,ABCD为竖直平面内固定的光滑轨道,其中AB段为斜面,BC段是水平的,CD段为半径R=0.2m的半圆,圆心为O,与水平面相切与C点,直径CD垂直于BC.现将小球甲从斜面上距BC高为$\frac{10}{3}$R的A点由静止释放,到达B点后只保留水平分速度沿水平面运动,与静止在C点小球乙发生弹性碰撞,已知甲、乙两球的质量均为m=1.0×10-2kg,重力加速度g取10m/s2.(水平轨道足够长,甲、乙两球可视为质点)求:
如图所示,ABCD为竖直平面内固定的光滑轨道,其中AB段为斜面,BC段是水平的,CD段为半径R=0.2m的半圆,圆心为O,与水平面相切与C点,直径CD垂直于BC.现将小球甲从斜面上距BC高为$\frac{10}{3}$R的A点由静止释放,到达B点后只保留水平分速度沿水平面运动,与静止在C点小球乙发生弹性碰撞,已知甲、乙两球的质量均为m=1.0×10-2kg,重力加速度g取10m/s2.(水平轨道足够长,甲、乙两球可视为质点)求:分析 (1)首先小球乙为研究对象,乙恰能通过轨道的最高点D,则重力恰好通过向心力,列出牛顿第二定律的方程;从C到D的过程中,小球乙的机械能守恒,列出方程,联立即可求出小球在C的速度,最后使用牛顿第二定律求出小球在C处受到的支持力,由牛顿第三定律说明即可.
(2)利用机械能守恒求出甲到达B点的速度,然后将速度分解,保留水平方向的分速度即为C点的速度;甲与乙碰撞的过程中动量守恒,能量守恒,联立方程即可求出斜面的倾角.
(3)增大甲的质量,保持乙的质量不变,则甲乙碰撞的过程中乙获得的速度增大,然后由机械能守恒求出小球乙通过C点的速度的范围,利用平抛运动求出平抛的水平距离 范围.
解答 解:(1)乙恰能通过轨道的最高点D,则重力恰好通过向心力,得:$mg=\frac{m{v}_{D}^{2}}{R}$
乙球从C到D的过程中机械能守恒,得:$\frac{1}{2}m{v}_{C}^{2}=2mgR+\frac{1}{2}m{v}_{D}^{2}$
联立以上两式得:${v}_{C}=\sqrt{5gR}$
乙球在C点受到的支持力与重力的合力提供向心加速度,得:${F}_{N}-mg=\frac{m{v}_{C}^{2}}{R}$
所以:${F}_{N}=mg+\frac{m{v}_{C}^{2}}{R}$=6×1.0×10-2N=0.6N
由牛顿第三定律可知,乙对半圆轨道最低点C处的压力与轨道对小球的支持力大小相等,即:F=FN=0.6N
(2)甲与乙的质量相同,所以甲与乙发生弹性碰撞的过程二者交换速度,所以甲到达C的速度等于乙在C点的速度,即:${v}_{甲x}={v}_{C}=\sqrt{5gR}$
甲从A滑到B的过程中机械能守恒,得:mgh=$\frac{1}{2}m{v}^{2}$
甲到达B点后只保留水平分速度沿水平面运动,则:v甲x=v•cosθ
所以:$cosθ=\frac{{v}_{甲x}}{v}$=$\frac{\sqrt{5gR}}{\sqrt{2gh}}=\frac{\sqrt{5gR}}{\sqrt{2g×\frac{10R}{3}}}=\frac{\sqrt{3}}{2}$
则:θ=30°
(3)将甲仍从A点释放,增大甲的质量为M,甲到达C的速度仍然是$\sqrt{5gR}$,保持乙的质量不变,仍然发生弹性碰撞,以向左为正方向,则:
动量守恒:MvC=Mv1+mv2
机械能守恒:$\frac{1}{2}M{v}_{C}^{2}=\frac{1}{2}M{v}_{1}^{2}+\frac{1}{2}m{v}_{2}^{2}$
联立解得:${v}_{1}=\frac{(M-m){v}_{C}}{M+m}$,${v}_{2}=\frac{2M{v}_{C}}{M+m}$
当甲的质量比乙的质量大很多是时候,乙球的速度最大,${v}_{2}=\frac{2M{v}_{C}}{M+m}=\frac{2{v}_{C}}{1+\frac{m}{M}}≈2{V}_{c}$,即最大速度约为原来速度的2倍.
乙离开圆轨道后做平抛运动,运动的时间:$t=\sqrt{\frac{2•2R}{g}}=2\sqrt{\frac{R}{g}}$
水平方向做匀速直线运动,速度最小时的水平方向的位移:${x}_{min}={v}_{C}•t=\sqrt{5gR}•2\sqrt{\frac{R}{g}}$=2×2.236×0.2=0.8944m
速度最大时的水平方向的位移:xmax=2vC•t=2xmin=1.7888m
答:(1)甲、乙碰后瞬间,乙对半圆轨道最低点C处的压力是0.6N;
(2)斜面与水平面的夹角是30°;
(3)若将甲仍从A点释放,增大甲的质量,保持乙的质量不变,乙在轨道上的首次落点到C点的距离范围是0.8944m≤x≤1.7888m.
点评 本题关键是明确两个小球的运动情况,然后分过程运用机械能守恒定律、动量守恒定律、平抛运动的分位移公式和向心力公式列式求解.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量为m=10kg的物块,在F=30N的水平拉力作用下,从静止开始沿水平面运动t1=4s后撤去拉力,已知物块与水平面间的动摩擦因数为μ=0.2,g取10m/s2.求:
如图所示,质量为m=10kg的物块,在F=30N的水平拉力作用下,从静止开始沿水平面运动t1=4s后撤去拉力,已知物块与水平面间的动摩擦因数为μ=0.2,g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
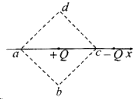 如图所示,在x轴上固定两个等量异种点电荷+Q、-Q,两点电荷之间距离L,虚线是以+Q所在点为中心,边长为L的正方形,a、b、c、d为正方形的四个顶点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )
如图所示,在x轴上固定两个等量异种点电荷+Q、-Q,两点电荷之间距离L,虚线是以+Q所在点为中心,边长为L的正方形,a、b、c、d为正方形的四个顶点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )| A. | 四点中c点处的电势最低 | |
| B. | a,b两点的电势差Uab大于a,d两点的电势差Uad | |
| C. | 将一正试探电荷沿a→b→c从a移至c点,电势能先增大后减小 | |
| D. | a点电场强度的大小Ea大于c点的电场强度的大小Ec |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
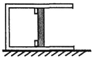 如图所示,一开口向右的气缸固定在水平地面上,活塞可无摩擦移动且不漏气,气缸中间位置有一挡板,外界大气压为P0.初始时,活塞紧压挡板处.现缓慢升高缸内气体温度,则图中能正确反应缸内气体压强变化情况的P-T图象是( )
如图所示,一开口向右的气缸固定在水平地面上,活塞可无摩擦移动且不漏气,气缸中间位置有一挡板,外界大气压为P0.初始时,活塞紧压挡板处.现缓慢升高缸内气体温度,则图中能正确反应缸内气体压强变化情况的P-T图象是( )| A. | 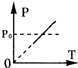 | B. | 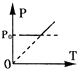 | C. | 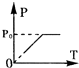 | D. | 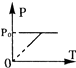 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
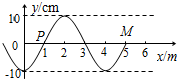 如图所示,一列简谐横波沿x轴正方向传播,从波传到x=5m的M点时开始计时,已知P点相继出现两个波峰的时间间隔为0.4s,下面说法中正确的是( )
如图所示,一列简谐横波沿x轴正方向传播,从波传到x=5m的M点时开始计时,已知P点相继出现两个波峰的时间间隔为0.4s,下面说法中正确的是( )| A. | 质点Q(x=9m,图中未画出)经过0.5s第一次到达波谷 | |
| B. | 质点P在0.1s内沿波传播方向的位移为1m | |
| C. | 若在Q处放一接收器,接到的波的频率小于2.5Hz | |
| D. | 若该波传播中遇到宽约3m的障碍物能发生明显的衍射现象 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 在“验证机械能守恒定律”的实验中,质量为m=1kg的重物自由下落,在纸带上打出一系列的点,如图所示(相邻计数点时间间隔为0.02s),单位为cm,那么:
在“验证机械能守恒定律”的实验中,质量为m=1kg的重物自由下落,在纸带上打出一系列的点,如图所示(相邻计数点时间间隔为0.02s),单位为cm,那么:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
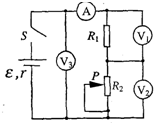 在如图所示电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,电表示数变化量的绝对值分别用△I、△U1、△U2和△U3表示.下列说法正确的是( )
在如图所示电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,电表示数变化量的绝对值分别用△I、△U1、△U2和△U3表示.下列说法正确的是( )| A. | $\frac{{U}_{1}}{I}$不变,$\frac{△{U}_{1}}{△I}$变大 | B. | $\frac{{U}_{2}}{I}$变大,$\frac{△{U}_{2}}{△I}$不变 | ||
| C. | $\frac{{U}_{3}}{I}$变大,$\frac{△{U}_{3}}{△I}$变大 | D. | 电源的输出功率变大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com