
 17世纪中,美国开始应用架空索道传送散状物料;19世纪中叶,各种现代结构的传送带输送机相继出现.此后,传送带输送机 受到机械制造、电机、化工和冶金工业技术进步的影响,不断完善,逐步由完成车间内部的传送,如图所示为木料厂的木料送装置,斜坡长为 L=20m,高为h=2m,斜坡上紧排着一排滚筒.长为l=8m、质量为m=1×100kg的木料ab放在滚筒上,木料与滚筒间的动摩擦因数为μ=0.3,滚筒边缘的线速度均为v=4m/s.滚筒转动由电动机控制,电动机关闭,滚筒立刻停止运动,木料对滚筒的总压力近似等于木料的重力.取当地的重力加速度g=10m/s2.
17世纪中,美国开始应用架空索道传送散状物料;19世纪中叶,各种现代结构的传送带输送机相继出现.此后,传送带输送机 受到机械制造、电机、化工和冶金工业技术进步的影响,不断完善,逐步由完成车间内部的传送,如图所示为木料厂的木料送装置,斜坡长为 L=20m,高为h=2m,斜坡上紧排着一排滚筒.长为l=8m、质量为m=1×100kg的木料ab放在滚筒上,木料与滚筒间的动摩擦因数为μ=0.3,滚筒边缘的线速度均为v=4m/s.滚筒转动由电动机控制,电动机关闭,滚筒立刻停止运动,木料对滚筒的总压力近似等于木料的重力.取当地的重力加速度g=10m/s2. =16 m
=16 m m/s
m/s s.
s.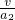 =1 s,匀减速运动位移x3=
=1 s,匀减速运动位移x3= t3=2 m
t3=2 m -x1-x3=10 m
-x1-x3=10 m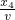 +t3=5.5 s
+t3=5.5 s

科目:高中物理 来源: 题型:
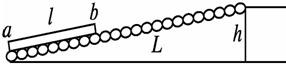 17世纪中,美国开始应用架空索道传送散状物料;19世纪中叶,各种现代结构的传送带输送机相继出现.此后,传送带输送机 受到机械制造、电机、化工和冶金工业技术进步的影响,不断完善,逐步由完成车间内部的传送,如图所示为木料厂的木料送装置,斜坡长为 L=20m,高为h=2m,斜坡上紧排着一排滚筒.长为l=8m、质量为m=1×100kg的木料ab放在滚筒上,木料与滚筒间的动摩擦因数为μ=0.3,滚筒边缘的线速度均为v=4m/s.滚筒转动由电动机控制,电动机关闭,滚筒立刻停止运动,木料对滚筒的总压力近似等于木料的重力.取当地的重力加速度g=10m/s2.
17世纪中,美国开始应用架空索道传送散状物料;19世纪中叶,各种现代结构的传送带输送机相继出现.此后,传送带输送机 受到机械制造、电机、化工和冶金工业技术进步的影响,不断完善,逐步由完成车间内部的传送,如图所示为木料厂的木料送装置,斜坡长为 L=20m,高为h=2m,斜坡上紧排着一排滚筒.长为l=8m、质量为m=1×100kg的木料ab放在滚筒上,木料与滚筒间的动摩擦因数为μ=0.3,滚筒边缘的线速度均为v=4m/s.滚筒转动由电动机控制,电动机关闭,滚筒立刻停止运动,木料对滚筒的总压力近似等于木料的重力.取当地的重力加速度g=10m/s2.查看答案和解析>>
科目:高中物理 来源:2011年浙江省高考物理模拟试卷(一)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com