碰撞的恢复系数的定义为
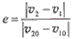
,其中v
10和v
20分别是碰撞前两物体的速度,v
1和v
2分别是碰撞后物体的速度。弹性碰撞的恢复系数e=1,非弹性碰撞的e<1。某同学借用验证动力守恒定律的实验装置(如图所示)验证弹性碰撞的恢复系数是否为1,实验中使用半径相等的钢质小球1和2(它们之间的碰撞可近似视为弹性碰撞),且小球1的质量大于小球2的质量。
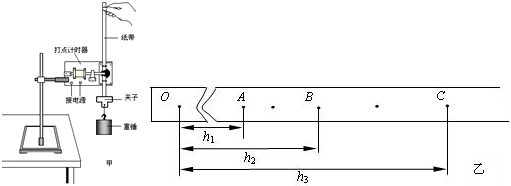
实验步骤如下:安装好实验装置,做好测量前的准备,并记下重锤线所指的位置O。
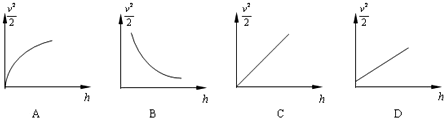
第一步,不放小球2,让小球1从斜槽上A点由静止滚下,并落在地面上。重复多次,用尽可能小的圆把小球的所落点圈在里面,其圆心就是小球落点的平均位置;
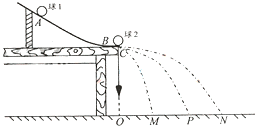
第二步,把小球2 放在斜槽前端边缘处C点,让小球1从A点由静止滚下,使它们碰撞。重复多次,并使用与第一步同样的方法分别标出碰撞后小球落点的平均位置;
第三步,用刻度尺分别测量三个落地点的平均位置离O点的距离,即线段OM、OP、ON的长度。
上述实验中:
(1)P点是________________平均位置,M点是________________平均位置,N点是________________平均位置。
(2)请写出本实验的原理________________,写出用测量量表示的恢复系数的表达式________________。
(3)三个落地点距O点的距离OM、OP、ON与实验所用的小球质量是否有关系?________________。

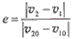 ,其中v10和v20分别是碰撞前两物体的速度,v1和v2分别是碰撞后物体的速度。弹性碰撞的恢复系数e=1,非弹性碰撞的e<1。某同学借用验证动力守恒定律的实验装置(如图所示)验证弹性碰撞的恢复系数是否为1,实验中使用半径相等的钢质小球1和2(它们之间的碰撞可近似视为弹性碰撞),且小球1的质量大于小球2的质量。
,其中v10和v20分别是碰撞前两物体的速度,v1和v2分别是碰撞后物体的速度。弹性碰撞的恢复系数e=1,非弹性碰撞的e<1。某同学借用验证动力守恒定律的实验装置(如图所示)验证弹性碰撞的恢复系数是否为1,实验中使用半径相等的钢质小球1和2(它们之间的碰撞可近似视为弹性碰撞),且小球1的质量大于小球2的质量。 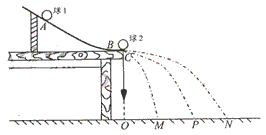

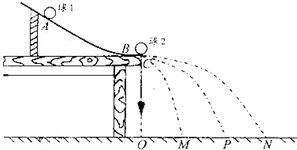 碰撞的恢复系数的定义为c=
碰撞的恢复系数的定义为c= (2007?浙江)(1)用示波器观察频率为900Hz的正弦电压信号.把该信号接入示波器Y输入.
(2007?浙江)(1)用示波器观察频率为900Hz的正弦电压信号.把该信号接入示波器Y输入.