
| A. | 该星球的密度是地球密度的2倍 | |
| B. | 该星球表面的重力加速度是地球表面重力加速度的4倍 | |
| C. | 该星球的近地卫星的速度是地球近地卫速度的4倍 | |
| D. | 该星球的近地卫星周期跟地球的近地卫星周期相等 |
分析 根据质量和体积的关系求出密度的关系.根据万有引力等于重力求出重力加速度的表达式,结合半径和质量之比求出重力加速度的关系.根据万有引力提供向心力得出线速度与周期的关系式,结合质量和半径关系求出线速度和周期的关系.
解答 解:A、根据$ρ=\frac{M}{V}$知,星球的半径是地球的2倍,则体积是地球体积的8倍,质量是地球的8倍,可知星球的密度与地球的密度相同,故A错误.
B、根据$G\frac{Mm}{{R}^{2}}=mg$得,g=$\frac{GM}{{R}^{2}}$,因为星球的质量是地球的8倍,半径是地球半径的2倍,则星球表面的重力加速度是地球表面重力加速度的2倍,故B错误.
C、根据v=$\sqrt{\frac{GM}{R}}$知,星球的质量是地球的8倍,半径是地球半径的2倍,则星球的近地卫星的速度是地球近地卫速度的2倍,故C错误.
D、根据$G\frac{Mm}{{R}^{2}}=mR\frac{4{π}^{2}}{{T}^{2}}$得,T=$\sqrt{\frac{4{π}^{2}{R}^{3}}{GM}}$,因为半径之比为2:1,质量之比为8:1,则周期相等,故D正确.
故选:D.
点评 解决本题的关键掌握万有引力定律的两个理论:1、万有引力提供向心力,2、万有引力等于重力,并能灵活运用.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中物理 来源: 题型:解答题
| 原子核 | 原子质量(u) |
| ${\;}_{2}^{4}$He | 4.0026 |
| ${\;}_{27}^{60}$Co | 59.9338 |
| ${\;}_{28}^{64}$Cu | 63.9298 |
| ${\;}_{92}^{208}$Pb | 207.9766 |
| ${\;}_{84}^{212}$Po | 211.9889 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
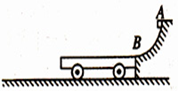 如图所示,AB为半径R=0.8m的$\frac{1}{4}$光滑圆弧轨道,下端B恰与小车右端平滑对接.小车质量M=3kg,车长L=2.06m,车上表面距地面的高度h=0.2m.现有一质量m=lkg的小滑块(可看成质点),由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5s时,车被地面装置锁定.(g=10m/s2)试求:
如图所示,AB为半径R=0.8m的$\frac{1}{4}$光滑圆弧轨道,下端B恰与小车右端平滑对接.小车质量M=3kg,车长L=2.06m,车上表面距地面的高度h=0.2m.现有一质量m=lkg的小滑块(可看成质点),由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5s时,车被地面装置锁定.(g=10m/s2)试求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 小明同学在学习了圆周运动的知识后,设计了测量自行车骑行速度的实验方案,他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.
小明同学在学习了圆周运动的知识后,设计了测量自行车骑行速度的实验方案,他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
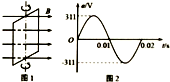 在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图1所示,产生的交变电动势的图象如图2所示,则( )
在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图1所示,产生的交变电动势的图象如图2所示,则( )| A. | t=0.015s时线框的电动势为零 | |
| B. | t=0.02s时线框平面与中性面垂直 | |
| C. | 线框产生的交变电动势有效值为311V | |
| D. | 该交变电动势瞬时值的表达式为e=311sin(100πt)V |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
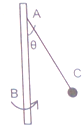 长为L的细线一端固定在如图所示的竖直杆上A点,另一端系一个质量为m的小球C,当竖直杆以一定的角速度绕AB轴匀速转动时,小球在水平面内做匀速圆周运动,细线与竖直方向的夹角为θ,重力加速度为g,求:
长为L的细线一端固定在如图所示的竖直杆上A点,另一端系一个质量为m的小球C,当竖直杆以一定的角速度绕AB轴匀速转动时,小球在水平面内做匀速圆周运动,细线与竖直方向的夹角为θ,重力加速度为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com