
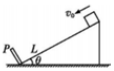
 足够长的倾角为θ的粗糙斜面上,有一质量为m的滑块距挡板P为L,以初速度v0沿斜面下滑,并与挡板发生碰撞,滑块与斜面动摩擦因数为μ,μ<tanθ.若滑块与挡板碰撞没有机械能损失,求:
足够长的倾角为θ的粗糙斜面上,有一质量为m的滑块距挡板P为L,以初速度v0沿斜面下滑,并与挡板发生碰撞,滑块与斜面动摩擦因数为μ,μ<tanθ.若滑块与挡板碰撞没有机械能损失,求:分析 (1)由功的定义式求解;
(2)对滑块下滑过程应用动能定理求得碰撞前的动能,然后对碰撞后上滑的过程应用动能定理即可求解;
(3)分析滑块受力情况,得到滑块的最终位置,然后对整个运动过程应用动能定理求解.
解答 解:(1)由功的定义式可知:滑块第一次与挡板碰撞时重力做的功为:
WG=mgLsinθ;
(2)对滑块下滑到滑块第一次与挡板碰撞的过程应用动能定理可得:
$mgLsinθ-μmgLcosθ=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$;
滑块与挡板碰撞没有机械能损失,故碰后滑块的动能仍为$\frac{1}{2}m{v}^{2}$;
对滑块第一次与挡板碰撞后上升的过程应用动能定理可得:
$-mgSsinθ-μmgScosθ=0-\frac{1}{2}m{v}^{2}$;
所以,滑块第一次与挡板碰撞后上升离开挡板P的最大距离为:
$S=\frac{\frac{1}{2}m{v}^{2}}{mg(sinθ+μcosθ)}$=$\frac{\frac{1}{2}m{{v}_{0}}^{2}+mgLsinθ-μmgLcosθ}{mg(sinθ+μcosθ)}$=$\frac{{{v}_{0}}^{2}+2gLsinθ-2μgLcosθ}{2g(sinθ+μcosθ)}$;
(3)μ<tanθ,所以,mgsinθ>μmgcosθ,故滑块最终停靠着挡板;
滑块运动过程只有摩擦力和重力做功,故由动能定理可得:
$mgLsinθ-μmg{s}_{总}cosθ=0-\frac{1}{2}m{{v}_{0}}^{2}$,
所以,滑块在整个运动过程中通过的路程为:
${s}_{总}=\frac{\frac{1}{2}m{{v}_{0}}^{2}+mgLsinθ}{μmgcosθ}$=$\frac{{{v}_{0}}^{2}+2gLsinθ}{2μgcosθ}$;
答:(1)滑块第一次与挡板碰撞时重力做的功为mgLsinθ;
(2)滑块第一次与挡板碰撞后上升离开挡板P的最大距离为$\frac{{{v}_{0}}^{2}+2gLsinθ-2μgLcosθ}{2g(sinθ+μcosθ)}$;
(3)滑块在整个运动过程中通过的路程为$\frac{{{v}_{0}}^{2}+2gLsinθ}{2μgcosθ}$.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.


科目:高中物理 来源: 题型:选择题
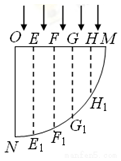 如图是一个$\frac{1}{4}$圆柱体棱镜的截面图,图中E、F、G、H将半径OM分成5等份,虚线EE1、FF1、GG1、HH1平行于半径ON,ON边可吸收到达其上的所有光线.已知该棱镜的折射率n=$\frac{5}{2}$,若平行光束垂直入射并覆盖OM,则光线( )
如图是一个$\frac{1}{4}$圆柱体棱镜的截面图,图中E、F、G、H将半径OM分成5等份,虚线EE1、FF1、GG1、HH1平行于半径ON,ON边可吸收到达其上的所有光线.已知该棱镜的折射率n=$\frac{5}{2}$,若平行光束垂直入射并覆盖OM,则光线( )| A. | 只能从圆孤NF1射出 | B. | 只能从圆孤NG1射出 | ||
| C. | 可能从圆孤G1H1射出 | D. | 可能从圆孤H1M射出 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
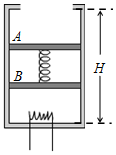 如图所示,导热气缸上端开口,竖直固定在地面上,高度H=1.05m.质量均为m=1kg的A、B两个活塞静止时将气缸容积均分为三等份,A、B之间为真空并压缩一根轻质弹簧,弹性系数k=400N/m,A、B与气缸间无摩擦.大气压P0=1×105Pa,密封气体初始温度T0=300K,重力加速度g取10m/s2,活塞面积S=2×10-3 m2,其厚度忽略不计.
如图所示,导热气缸上端开口,竖直固定在地面上,高度H=1.05m.质量均为m=1kg的A、B两个活塞静止时将气缸容积均分为三等份,A、B之间为真空并压缩一根轻质弹簧,弹性系数k=400N/m,A、B与气缸间无摩擦.大气压P0=1×105Pa,密封气体初始温度T0=300K,重力加速度g取10m/s2,活塞面积S=2×10-3 m2,其厚度忽略不计.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
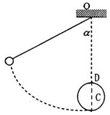 长为L的轻绳一端系一小球(可视为质点),另一端悬于O点.小球从与竖直方向成60°角处释放,到最低点与一钉子C相碰后绕C做圆周运动,欲使小球刚好能通过最高点,则钉子距悬点O的距离h为多大.(不计空气阻力)
长为L的轻绳一端系一小球(可视为质点),另一端悬于O点.小球从与竖直方向成60°角处释放,到最低点与一钉子C相碰后绕C做圆周运动,欲使小球刚好能通过最高点,则钉子距悬点O的距离h为多大.(不计空气阻力)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 20J、5W | B. | 20J、10W | C. | 40J、10W | D. | 40J、20W |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 2016年9月15日,“天宫二号”空间实验室在酒泉卫星发射中心发射成功.“天宫二号”是中国第一个真正意义上的空间实验室.在“天宫二号”除了要验证航天员在轨中期驻留,还将开展14项空间科学和应用实验.10月19日“神州十一号”飞船与在距地面高度为h的圆轨道上运行的“天宫二号”教会对接成功,航天员景海鹏、陈冬进入“天宫二号”.航天员此次在“天宫二号”中期驻留时间为t.
2016年9月15日,“天宫二号”空间实验室在酒泉卫星发射中心发射成功.“天宫二号”是中国第一个真正意义上的空间实验室.在“天宫二号”除了要验证航天员在轨中期驻留,还将开展14项空间科学和应用实验.10月19日“神州十一号”飞船与在距地面高度为h的圆轨道上运行的“天宫二号”教会对接成功,航天员景海鹏、陈冬进入“天宫二号”.航天员此次在“天宫二号”中期驻留时间为t.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
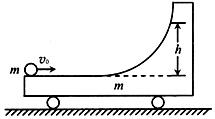 如图所示,质量为m的小车静置于光滑水平面上,小车右端带有光滑圆弧轨道,一质量也为m的小球以水平速度v0从左端冲上小车,到达某一高度h后又能回到小车左端,重力加速度为g,不计一切摩擦,以下说法正确的是( )
如图所示,质量为m的小车静置于光滑水平面上,小车右端带有光滑圆弧轨道,一质量也为m的小球以水平速度v0从左端冲上小车,到达某一高度h后又能回到小车左端,重力加速度为g,不计一切摩擦,以下说法正确的是( )| A. | 小球回到小车左端时速度为v0 | B. | 小球回到小车左端时速度为0 | ||
| C. | $h=\frac{v_0^2}{2g}$ | D. | $h=\frac{v_0^2}{4g}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
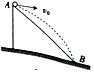 如图所示,小球从斜面的顶端A处以大小为v0的初速度水平抛出,恰好落到斜面底部的B点,且此时的速度大小vB=$\sqrt{5}$v0,空气阻力不计,该斜面的倾角为( )
如图所示,小球从斜面的顶端A处以大小为v0的初速度水平抛出,恰好落到斜面底部的B点,且此时的速度大小vB=$\sqrt{5}$v0,空气阻力不计,该斜面的倾角为( )| A. | 30° | B. | 37° | C. | 45° | D. | 60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com