
【题目】某中学生小明想探究拉力做功与弹簧弹性势能增量的关系。如图所示,轻弹簧左端固定,被外力从原长A位置开始拉长到B位置。小明发现拉力是一个越来越大的变力,所以描绘了拉力和弹簧伸长量的变化图像(如图),并且发现该图像为过坐标原点O的直线,实验过程中,弹簧始终处于弹性限度内。
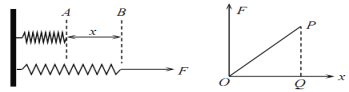
(1)根据所学知识,可以判断直角三角形PQO的面积的物理意义是:___________
(2)由此可推断,如果一劲度系数为k的轻弹簧,在弹性限度内,当其形变大小为x时,弹簧的弹性势能的表达式为Ep=_______________。
科目:高中物理 来源: 题型:
【题目】如图所示,倾角![]() 、长L=4.5 m的斜面,底端与一个光滑的
、长L=4.5 m的斜面,底端与一个光滑的![]() 圆弧轨道平滑连接,圆弧轨道底端切线水平,一质量为m=1 kg的物块(可视为质点)从斜面最高点A由静止开始沿斜面下滑,经过斜面底端B后恰好能到达圆弧轨道最高点C,又从圆弧轨道滑回,能上升到斜面上的D点,再由D点由斜面下滑沿圆弧轨道上升,再滑回,这样往复运动,最后停在B点。已知物块与斜面间的动摩擦因数为
圆弧轨道平滑连接,圆弧轨道底端切线水平,一质量为m=1 kg的物块(可视为质点)从斜面最高点A由静止开始沿斜面下滑,经过斜面底端B后恰好能到达圆弧轨道最高点C,又从圆弧轨道滑回,能上升到斜面上的D点,再由D点由斜面下滑沿圆弧轨道上升,再滑回,这样往复运动,最后停在B点。已知物块与斜面间的动摩擦因数为![]() ,g=10 m/s2,假设物块经过斜面与圆弧轨道平滑连接处速率不变。求:
,g=10 m/s2,假设物块经过斜面与圆弧轨道平滑连接处速率不变。求:
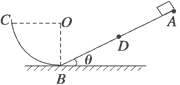
(1)物块经多长时间第一次到B点;
(2)物块第一次经过B点时对圆弧轨道的压力;
(3)物块在斜面上滑行的总路程。
查看答案和解析>>
科目:高中物理 来源: 题型:
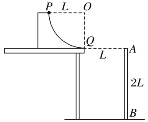
【题目】探究平抛运动实验装置如图所示,半径为 L 的四分之一圆轨道(可视为光滑) 固定于水平桌面上,切口水平且与桌边对齐,切口离地面高度为 2L.离切口水平距离为 L 的一探测屏 AB 竖直放置,一端放在水平面上,其高为 2L.一质量为 m 的小球从圆轨道上不同的位置静止释放打在探测屏上.若小球在运动过程中空气阻力不计,小球可视为质点, 重力加速度为 g.求:
(1)小球从图示位置 P 处静止释放,到达圆轨道最低点 Q 处速度大小及小球对圆轨道压力;
(2)为让小球能打在探测屏上,小球应从圆轨道上什么范围内静止释放?
(3)小球从什么位置静止释放,小球打在屏上时动能最小,最小动能为多少?
查看答案和解析>>
科目:高中物理 来源: 题型:
【题目】(多选)地球同步卫星因为其轨道远高于近地卫星,所以发射的难度更大,全球只有不多的几个国家有能力发射同步卫星。发射同步卫星时,卫星首先进入近地轨道(图中未画出),然后变轨进入椭圆轨道Ⅰ,最后在Q点通过改变卫星速度进行变轨,最终让卫星进入地球同步轨道Ⅱ,则( )
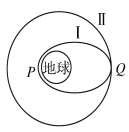
A. 该卫星在轨道Ⅰ上运行到P点时的速度大于7.9 km/s,小于11.2 km/s
B. 卫星在同步轨道Ⅱ上的运行速度大于7.9 km/s
C. 在轨道Ⅰ上,卫星在P点的速度大于在Q点的速度
D. 卫星在Q点通过加速实现由轨道Ⅰ进入轨道Ⅱ
查看答案和解析>>
科目:高中物理 来源: 题型:
【题目】一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定,有质量相同的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,如图所示,A的运动半径较大,则( )
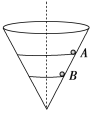
A. A球的角速度必小于B球的角速度B. A球的运动周期必等于B球的运动周期
C. A球的线速度必大于B球的线速度D. A球对筒壁的压力必大于B球对筒壁的压力
查看答案和解析>>
科目:高中物理 来源: 题型:
【题目】某同学利用如图甲所示的实验装置,测定物块与水平桌面间的动摩擦因数.物块在重物的牵引下开始运动,重物落地后,物块再运动一段距离停在桌面上(尚未到达滑轮处).从纸带上便于测量的点开始,每5个点取1个计数点,按照打点先后顺序进行标记计数点1、2、3…,相邻计数点间的距离如图乙所示.打点计时器电源的频率为50 Hz.

(1)通过分析纸带数据,可判断物块在两相邻计数点___________和__________之间某时刻重物落地.
(2)重物落地后,物块加速度的大小约为a=________m/s2(保留3位有效数字).
(3)物块和水平桌面间的动摩擦因数μ=________(保留1位小数).
查看答案和解析>>
科目:高中物理 来源: 题型:
【题目】一束光从空气射向折射率n=![]() 的某种玻璃的表面,如图所示.θ1代表入射角,则
的某种玻璃的表面,如图所示.θ1代表入射角,则
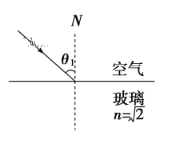
A. 当θ1>45°时会发生全反射现象
B. 无论入射角θ1是多大,折射角θ2都不会超过45°
C. 当入射角θ1=60°时,折射角θ2=30°
D. 当入射角θ1=60°时,反射光线与折射光线垂直
查看答案和解析>>
科目:高中物理 来源: 题型:
【题目】如图,a、b、c是在地球大气层外圆轨道上运动的3颗卫星,下列说法正确的是( )

A. b、c的线速度大小相等,且大于a的线速度
B. b、c的向心加速度大小相等,且大于a的向心加速度
C. c加速可追上同一轨道上的b,b减速可等候同一轨道上的c
D. a卫星由于某原因,轨道半径缓慢减小,其线速度将增大
查看答案和解析>>
科目:高中物理 来源: 题型:
【题目】如图所示,在竖直平面(纸面)内有一直角坐标系xOy,水平轴x下方有垂直纸面向里的匀强磁场,第三象限有沿x轴负方向的匀强电场,第四象限存在另一匀强电场(图中未画出);光滑绝缘的固定不带电细杆PQ交x轴于M点,细杆PQ与x轴的夹角θ=30°,杆的末端在y轴Q点处,PM两点间的距离为L。一套在杆上的质量为2m、电荷量为q的带正电小环b恰好静止在M点,另一质量为m、不带电绝缘小环a套在杆上并由P点静止释放,与b瞬间碰撞后反弹,反弹后到达最高点时被锁定,锁定点与M点的距离为![]() ,b沿杆下滑过程中始终与杆之间无作用力,b进入第四象限后做匀速圆周运动,而后通过x轴上的N点,且OM=ON。已知重力加速度大小为g,求:
,b沿杆下滑过程中始终与杆之间无作用力,b进入第四象限后做匀速圆周运动,而后通过x轴上的N点,且OM=ON。已知重力加速度大小为g,求:

(1)碰后b的速度大小υ以及a、b碰撞过程中系统损失的机械能△E;
(2)磁场的磁感应强度大小B;
(3)b离开杆后经过多长时间会通过x轴。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com