
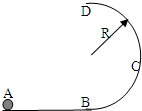
 如图所示,竖直的半圆型光滑轨道与水平轨道相切,轨道半径R=0.2m.质量m=0.2kg的小球以某一速度正对半圆型轨道运动,B、D两点分别是半圆轨道的最低点和最高点,小球经过B点的速度为vB=5m/s,达到D点时加速度的大小为4.5g,求:(取
如图所示,竖直的半圆型光滑轨道与水平轨道相切,轨道半径R=0.2m.质量m=0.2kg的小球以某一速度正对半圆型轨道运动,B、D两点分别是半圆轨道的最低点和最高点,小球经过B点的速度为vB=5m/s,达到D点时加速度的大小为4.5g,求:(取 =1.4 )
=1.4 )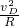 ,得到vD=
,得到vD=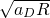 =3m/s.
=3m/s.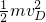 =
=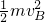
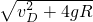 =
=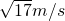
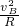



科目:高中物理 来源: 题型:
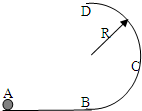
 如图所示,竖直的半圆型光滑轨道与水平轨道相切,轨道半径R=0.2m.质量m=0.2kg的小球以某一速度正对半圆型轨道运动,B、D两点分别是半圆轨道的最低点和最高点,小球经过B点的速度为vB=5m/s,达到D点时加速度的大小为4.5g,求:(取
如图所示,竖直的半圆型光滑轨道与水平轨道相切,轨道半径R=0.2m.质量m=0.2kg的小球以某一速度正对半圆型轨道运动,B、D两点分别是半圆轨道的最低点和最高点,小球经过B点的速度为vB=5m/s,达到D点时加速度的大小为4.5g,求:(取| 2 |
查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
| 2 |
查看答案和解析>>
科目:高中物理 来源:期中题 题型:计算题

查看答案和解析>>
科目:高中物理 来源:2010-2011学年湖北省黄冈市浠水县普通高中高一(下)期中物理试卷(解析版) 题型:解答题
 =1.4 )
=1.4 )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com