
分析 在客车与货车速度相等时,是它们的距离最小的时候,如果此时没有相撞,那就不可能在相撞了,分析这时它们的距离来判断是否会相撞.
解答 解:(1)设经时间t客车速度与货车相等,则有:由V=V0+at,
代入数据解得:t=25s,
此时,客车的位移为:
S客=Vt+$\frac{1}{2}$at2 =30×25+$\frac{1}{2}×0.8×2{5}^{2}$=1000m,
货车的位移为:
S货=V0t=10×25=250m,
因为S客>S货+S,所以会相撞.
(2)要使二者恰好不相撞;则有:
$\frac{{v}^{2}-{v}_{0}^{2}}{2a}$=200+v0$\frac{v-{v}_{0}}{a}$
代入数据解得:a=4m/s2;
答:(1)客车与货车相撞;
(2)客车加速度至少为4m/s2时才能避免相撞.
点评 本题考查追及相遇问题,要注意明确相撞的条件同时出现在同一个地点;根据条件列方程即可求解.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中物理 来源: 题型:多选题
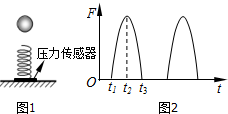 如图1所示,质量不计的弹簧竖直固定在水平面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球接触弹簧并将弹簧压缩至最低点(形变在弹性限度内),然后又被弹起离开弹簧,上升到一定高度后又下落,如此反复.通过安装在弹簧下端的压力传感器,测出该过程中弹簧弹力F随时间t变化的图象如图2所示,则( )
如图1所示,质量不计的弹簧竖直固定在水平面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球接触弹簧并将弹簧压缩至最低点(形变在弹性限度内),然后又被弹起离开弹簧,上升到一定高度后又下落,如此反复.通过安装在弹簧下端的压力传感器,测出该过程中弹簧弹力F随时间t变化的图象如图2所示,则( )| A. | 整个运动过程中小球的机械能守恒 | |
| B. | t2时刻小球的加速度为零 | |
| C. | t1~t2这段时间内,小球的动能先增加后减少 | |
| D. | t2~t3这段时间内,弹簧的弹性势能一直减少 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 元电荷是表示跟电子所带电荷量数值相等的电荷量 | |
| B. | 带电体体积很大时不能看成点电荷 | |
| C. | 摩擦起电说明电荷可以被创造 | |
| D. | 根据场强叠加原理,可知合电场的场强一定大于分电场的场强 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
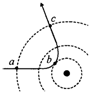 历史上英国物理学家卢瑟福根据α粒子(氦原子核)散射实验,提出了原子的核式结构模型.图中虚线表示原子核所形成的电场的等势线,实线表示一个α粒子的运动迹.在α粒子从a运动到b再运动到c的过程中,下列说法中正确的是( )
历史上英国物理学家卢瑟福根据α粒子(氦原子核)散射实验,提出了原子的核式结构模型.图中虚线表示原子核所形成的电场的等势线,实线表示一个α粒子的运动迹.在α粒子从a运动到b再运动到c的过程中,下列说法中正确的是( )| A. | 动能先增大,后减小 | |
| B. | 电势能先减小,后增大 | |
| C. | 电场力先做负功,后做正功,总功等于零 | |
| D. | 加速度先变大,后变小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,电容器两极板之间的距离为d,板间电压为U,极板间的匀强磁场的磁感应强度为B1,一束电荷量相同的带正电的粒子沿图示虚线方向射入电容器,沿直线穿过电容器后从D缝进入另一磁感应强度为B2的匀强磁场,结果分别垂直打在a、b两点,两点间距离为△R.设粒子所带电量为q,且不计粒子所受重力,求打在a、b两点的粒子的质量之差.
如图所示,电容器两极板之间的距离为d,板间电压为U,极板间的匀强磁场的磁感应强度为B1,一束电荷量相同的带正电的粒子沿图示虚线方向射入电容器,沿直线穿过电容器后从D缝进入另一磁感应强度为B2的匀强磁场,结果分别垂直打在a、b两点,两点间距离为△R.设粒子所带电量为q,且不计粒子所受重力,求打在a、b两点的粒子的质量之差.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | f1方向向下,f2方向向上,且f1=f2 | B. | f1方向向下,f2方向向上,且f1>f2 | ||
| C. | f1方向向上,f2方向向上,且f1=f2 | D. | f1方向向下,f2方向向下,且f1=f2 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
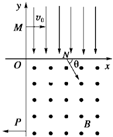 在平面直角坐标系xOy中,第Ⅰ象限存在沿y轴方向的匀强电场,第Ⅳ象限存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示.不计粒子重力,求:
在平面直角坐标系xOy中,第Ⅰ象限存在沿y轴方向的匀强电场,第Ⅳ象限存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示.不计粒子重力,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
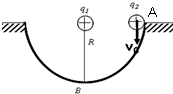 如图所示,竖直放置的半圆形光滑轨道半径为R,将带电量为+q1的点电荷固定于其圆心O处.另一带电量为+q2,质量为m的小球(可看作质点),从轨道上与圆心等高的A处以竖直向下的初速度vo开始沿轨道运动,(已知静电力常量为k).求:
如图所示,竖直放置的半圆形光滑轨道半径为R,将带电量为+q1的点电荷固定于其圆心O处.另一带电量为+q2,质量为m的小球(可看作质点),从轨道上与圆心等高的A处以竖直向下的初速度vo开始沿轨道运动,(已知静电力常量为k).求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
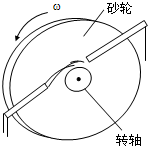 探究能力是物理学研究的重要能力之一,物体因绕轴转动而具有的动能叫转动动能,转动动能的大小与物体转动的角速度有关.为了研究某一砂轮的转动动能EK与角速度ω的关系,某同学采用了下述实验方法进行探索:(如图)先让砂轮由动力带动匀速旋转测得其角速度ω,然后让砂轮脱离动力,由于克服转轴间摩擦力做功,砂轮最后停下,测出砂轮脱离动力到停止转动的圈数n,通过分析实验数据,得出结论,经实验测得的几组ω和n如表所示:
探究能力是物理学研究的重要能力之一,物体因绕轴转动而具有的动能叫转动动能,转动动能的大小与物体转动的角速度有关.为了研究某一砂轮的转动动能EK与角速度ω的关系,某同学采用了下述实验方法进行探索:(如图)先让砂轮由动力带动匀速旋转测得其角速度ω,然后让砂轮脱离动力,由于克服转轴间摩擦力做功,砂轮最后停下,测出砂轮脱离动力到停止转动的圈数n,通过分析实验数据,得出结论,经实验测得的几组ω和n如表所示:| ω/rad•s-1 | 0.5 | 1 | 2 | 3 |
| EK/J | 5.0 | 20 | 80 | 180 |
| EK/J |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com