
 如图所示,质量m=1kg的小物体从倾角θ=37°的光滑斜面上A点静止开始下滑,经过B点后进入粗糙水平面(经过B点时速度大小不变而方向变为水平).AB=3m.试求:
如图所示,质量m=1kg的小物体从倾角θ=37°的光滑斜面上A点静止开始下滑,经过B点后进入粗糙水平面(经过B点时速度大小不变而方向变为水平).AB=3m.试求: =gsinθ=6m/s2
=gsinθ=6m/s2 ,得t1=1s,
,得t1=1s, =16.7N
=16.7N ≥F≥2N
≥F≥2N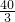 N≥F≥2N.
N≥F≥2N.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中物理 来源: 题型:
 如图所示,质量M=1.0kg的木块随传送带一起以v=2.0m/s的速度向左匀速运动,木块与传送带间的动摩擦因数μ=0.50.当木块运动至最左端A点时,一颗质量m=20g的子弹以v0=3.0×102m/s水平向右的速度击穿木块,穿出木块时的速度v1=50m/s.设传送带的速度始终恒定,子弹击穿木块的时间极短,且不计木块质量变化,g=10m/s2.求:
如图所示,质量M=1.0kg的木块随传送带一起以v=2.0m/s的速度向左匀速运动,木块与传送带间的动摩擦因数μ=0.50.当木块运动至最左端A点时,一颗质量m=20g的子弹以v0=3.0×102m/s水平向右的速度击穿木块,穿出木块时的速度v1=50m/s.设传送带的速度始终恒定,子弹击穿木块的时间极短,且不计木块质量变化,g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,质量m=1.0kg的小球B静止在平台上,平台高h=0.8m.一个质量M=2.0kg的小球A沿平台自左向右运动,与小球B处发生正碰,碰后小球B的速度vB=6.0m/s,小球A落在水平地面的C点,DC间距离s=1.2m.求:
如图所示,质量m=1.0kg的小球B静止在平台上,平台高h=0.8m.一个质量M=2.0kg的小球A沿平台自左向右运动,与小球B处发生正碰,碰后小球B的速度vB=6.0m/s,小球A落在水平地面的C点,DC间距离s=1.2m.求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,质量m=1.0kg的物体静止水平面上,水平恒力F=3.0作用于物体上,使物体从静止开始运动,经时间t=2.0s撤去拉力F,已知物体与水平面间的动摩擦因数μ=0.15,取g=10m/s2.求:
如图所示,质量m=1.0kg的物体静止水平面上,水平恒力F=3.0作用于物体上,使物体从静止开始运动,经时间t=2.0s撤去拉力F,已知物体与水平面间的动摩擦因数μ=0.15,取g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,质量M=1.0kg,长L=l.0m的木板静止在粗糙的水平地面上,木板与地面间的动摩擦因数μ1=0.1kg.在木板的左端放置一个质量m=1.0kg、大小可以忽略的铁块,铁块与木板间的动摩擦因数μ2=0.4.认为最大静摩擦力等于滑动摩擦力,取g=10m/s2.若在铁块上加一个水平向右的恒力F=8.0N,求:
如图所示,质量M=1.0kg,长L=l.0m的木板静止在粗糙的水平地面上,木板与地面间的动摩擦因数μ1=0.1kg.在木板的左端放置一个质量m=1.0kg、大小可以忽略的铁块,铁块与木板间的动摩擦因数μ2=0.4.认为最大静摩擦力等于滑动摩擦力,取g=10m/s2.若在铁块上加一个水平向右的恒力F=8.0N,求:查看答案和解析>>
科目:高中物理 来源: 题型:
| 1 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com