
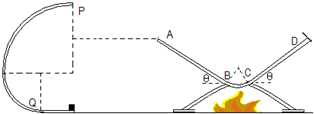
���� ��1������ţ�ٵڶ������������ǡ�õ���P����ٶȣ������ٶȷ�����б��ABƽ�У����ƽ���˶��Ĺ��ɣ�����ƽ���ı��ζ��������ֱ���ٶȣ��Ӷ��ó�AD��صĸ߶ȣ�
��2������ƽ���ı��ζ����������A��ʱ������ٶȣ���ȫ�������ö��ܶ�������������ڹ���б�����߹�����·�̣�
��3������ţ�ٵڶ����ɷֱ����P��Q�ĵ�������ϻ�е���غ㶨�ɵó�ѹ��������ߵ����С�ٶ����ѹ��֮�����Сֵ��
��� �⣺��1����P�㣬�� mg=m$\frac{{v}_{P}^{2}}{2R}$����ã�vP=$\sqrt{2gR}$
����A��ʱ�ٶȷ���Ҫ����AB��vy=vPtan��=$\frac{3}{4}\sqrt{2gR}$
����AD��ظ߶�Ϊ h=3R-$\frac{{v}_{y}^{2}}{2g}$=$\frac{39}{16}$R
��2������A�㻬����ٶ�Ϊ v=$\frac{{v}_{P}}{cos��}$=$\frac{5}{4}\sqrt{2gR}$
���辭��һ�������ܹ��ص�A�㣬�����ʱ����ΪEk�����
EK=$\frac{1}{2}$mv2-��mgcos��•8R��0
���Ի��鲻�Ử��A���ɳ���������BC�����ػ���
���ݶ��ܶ�����
mg•2Rsin��-��mgcos��s=0-$\frac{1}{2}$mv2
�������ݵã�1.2mgR-0.2mgs=-$\frac{25}{16}$mgR
��û����ڹ���б�����߹�����·�� s=$\frac{221}{16}$R
��3������ٶȡ���ߵ��ٶȷֱ�Ϊv1��v2����ţ�����ɣ���Q���У�
F1-mg=m$\frac{{v}_{1}^{2}}{R}$
��ã�F1=mg+m$\frac{{v}_{1}^{2}}{R}$
��P����F2+mg=m$\frac{{v}_{2}^{2}}{2R}$��
��ã�F2=m$\frac{{v}_{2}^{2}}{2R}$-mg
������F1-F2=2mg+$\frac{m��2{v}_{1}^{2}-2{v}_{2}^{2}+{v}_{2}^{2}��}{2R}$
�ɻ�е���غ�ã�
$\frac{1}{2}$mv12=$\frac{1}{2}$mv22+mg•3R��
��ã�v12-v22=6gRΪ��ֵ��
����v2����Сֵ $\sqrt{2gR}$����ѹ�������СֵΪ9mg��
��
��1��б���A��D����ظ�Ϊ$\frac{39}{16}$R��
��2�������ڹ���б����ͨ������·��Ϊ$\frac{221}{16}$R��
��3��ͨ����ߵ�P��СԲ����͵�Qʱ��ѹ��֮�����СֵΪ9mg��
���� ����ؼ�Ҫ����С����˶����������P����ٽ���������ȷ����״̬֮��Ĺ�ϵ�����ϻ�е���غ㣮����ƽ���˶������ܶ�������е���غ㡢ţ���˶����ɵȻ������ɴ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
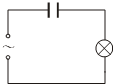 ��ͼ��ʾ��һƽ�а��������һ�����ݴ��������ڽ�����Դ�ϣ������������⣬������Щ����е��ݻ�䰵��������
��ͼ��ʾ��һƽ�а��������һ�����ݴ��������ڽ�����Դ�ϣ������������⣬������Щ����е��ݻ�䰵��������| A�� | ��С���������Ƶ�� | |
| B�� | �����������������糣��Ϊ�ŵĵ���� | |
| C�� | ��������������������� | |
| D�� | ���������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
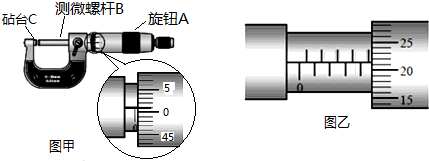
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
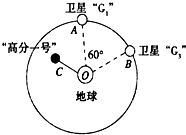 2014��3��8���賿�����ͻ�ʧ�����������Dz�����Ľ������������ơ��߷֡�ң��4���ͺŽ�10�����ǣ�Ϊ�����Ѿ��ṩ����֧�֣��ر��ǡ��߷�һ�š�ͻ���˿ռ�ֱ��ʡ���������������ϵĴ����ؼ���������ͼΪ���߷�һ�š��뱱������ϵͳ���������ڿ���ijһ�����˶���ʾ��ͼ��������ϵͳ���������ǡ�G1���͡�G3���Լ����߷�һ�š�������Ϊ�Ƶ���O������Բ���˶������ǡ�G1���͡�G3���Ĺ���뾶��Ϊr��ijʱ�����Ź������Ƿֱ�Ϊ����ϵ�A��B��λ�ã��߷�һ����Cλ�ã������Ǿ�˳ʱ�����У�������洦���������ٶ�Ϊg������뾶ΪR���������Ǽ�����������������˵����ȷ���ǣ�������
2014��3��8���賿�����ͻ�ʧ�����������Dz�����Ľ������������ơ��߷֡�ң��4���ͺŽ�10�����ǣ�Ϊ�����Ѿ��ṩ����֧�֣��ر��ǡ��߷�һ�š�ͻ���˿ռ�ֱ��ʡ���������������ϵĴ����ؼ���������ͼΪ���߷�һ�š��뱱������ϵͳ���������ڿ���ijһ�����˶���ʾ��ͼ��������ϵͳ���������ǡ�G1���͡�G3���Լ����߷�һ�š�������Ϊ�Ƶ���O������Բ���˶������ǡ�G1���͡�G3���Ĺ���뾶��Ϊr��ijʱ�����Ź������Ƿֱ�Ϊ����ϵ�A��B��λ�ã��߷�һ����Cλ�ã������Ǿ�˳ʱ�����У�������洦���������ٶ�Ϊg������뾶ΪR���������Ǽ�����������������˵����ȷ���ǣ�������| A�� | ���ǡ�G1���͡�G3���ļ��ٶȴ�С��Ⱦ�Ϊ$\frac{{R}^{2}}{r}$g | |
| B�� | ���ǡ�G1����λ��A�˶���λ��B����Ҫ��ʱ��Ϊ$\frac{2��r}{3R}$$\sqrt{\frac{r}{R}}$ | |
| C�� | ����������߷�һ�š����ǵ������ǡ�G3�����ڵĹ�������������� | |
| D�� | �߷�һ���ǵ�����ǣ������ڸ߶���ϡ�����壬����һ��ʱ��߶Ȼή�ͣ��ٶ�����е�ܻ��С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
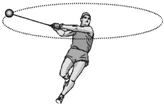 �������˶��У��˶�Աʹ���������ת����ˮƽ������Բ���˶���Ȼ��ͻȻ���֣����ڹ��ԣ�������Զ����ȥ��������Բ���˶��İ뾶ΪR��������ˮƽ������Բ���˶�ʱ����ظ߶�Ϊh����Բ���ڵ����ͶӰ��ΪO���������ص�ΪP��O��P����ľ��뼴Ϊ�˶�Ա�ijɼ������˶�Աij��������ijɼ�ΪL�������������Բ��ƣ���������˶�Ա�����ѿ�ʱ���ٶ�vΪ��������
�������˶��У��˶�Աʹ���������ת����ˮƽ������Բ���˶���Ȼ��ͻȻ���֣����ڹ��ԣ�������Զ����ȥ��������Բ���˶��İ뾶ΪR��������ˮƽ������Բ���˶�ʱ����ظ߶�Ϊh����Բ���ڵ����ͶӰ��ΪO���������ص�ΪP��O��P����ľ��뼴Ϊ�˶�Ա�ijɼ������˶�Աij��������ijɼ�ΪL�������������Բ��ƣ���������˶�Ա�����ѿ�ʱ���ٶ�vΪ��������| A�� | L$\sqrt{\frac{g}{2h}}$ | B�� | R$\sqrt{\frac{g}{2h}}$ | C�� | $\sqrt{\frac{g}{2h}��{L}^{2}-{R}^{2}��}$ | D�� | $\sqrt{\frac{g}{2h}��{L}^{2}+{R}^{2}��}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
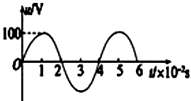
| A�� | �ý�����ĵ�ѹ˲ʱֵ�ı���ʽΪ u=100sin��50��t��V | |
| B�� | ��t=10-2sʱ����ͨ����� | |
| C�� | ��t=10-2sʱ����Ȧת�������д�ͨ���仯��Ϊ100wb/s | |
| D�� | �����ý�����ѹ������ֵΪR=100�� �ĵ������ˣ���������ĵĹ�����50W |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
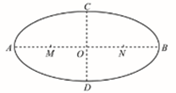 ��ͼ��ʾ����һˮƽ��Բ�����M��NΪ����Բ������������㣬����AB��CD�ֱ�Ϊ��Բ�ij���Ͷ��ᣬ�ཻ��O�㣬��AM=MO=OC=2cm��������˵����ȷ���ǣ�������
��ͼ��ʾ����һˮƽ��Բ�����M��NΪ����Բ������������㣬����AB��CD�ֱ�Ϊ��Բ�ij���Ͷ��ᣬ�ཻ��O�㣬��AM=MO=OC=2cm��������˵����ȷ���ǣ�������| A�� | ����+Q�ĵ��ɷ�����O�㣬��A��B�������ơ���ǿ����ͬ | |
| B�� | ����+Q��-Q�������ֵ�ɷֱ������M��N�㣬����������̽�����O���ĵ�����С��B���ĵ����� | |
| C�� | ����C����ֹ�ͷŵĵ��ӽ��ڵ糡������������CD���������˶����������M��N�ĵ��ɵ���Խ���������˶�������Խ�� | |
| D�� | ����һƽ���ڹ��ƽ�����ǿ�糡��A��B��C����ĵ��Ʒֱ�Ϊ10V��2V��8V������ǿ�糡��ǿΪ100$\sqrt{2}$V/m |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com