
| A. | 它们的向心力大小相等 | |
| B. | 它们的向心加速度大小相等 | |
| C. | 质量大的恒星的轨道半径大于质量小的恒星的轨道半径 | |
| D. | 质量大的恒星的动能小于质量小的恒星的动能 |
分析 抓住双星模型转动的周期、加速度相等,根据万有引力提供向心力列式分析即可.
解答 解:A、它们的向心力由万有引力提供,大小相等、方向相反,故A正确;
B、两个星的向心力相等,根据a=$\frac{F}{m}$,由于质量不等,故向心加速度不等,故B错误;
C、设m1的轨道半径为R1,m2的轨道半径为R2.两星之间的距离为L.
由于它们之间的距离恒定,因此双星在空间的绕向一定相同,同时角速度和周期也都相同.
根据万有引力提供向心力得:
$\frac{{G{m_1}{m_2}}}{L^2}={m_1}{R_1}\frac{{4{π^2}}}{T^2}$
$\frac{{G{m_1}{m_2}}}{L^2}={m_2}{R_2}\frac{{4{π^2}}}{T^2}$
其中:R1十R2=L
解得:
${R_1}=\frac{m_2}{{{m_1}+{m_2}}}L$
${R_2}=\frac{m_1}{{{m_1}+{m_2}}}L$
故质量大的恒星的轨道半径小,质量小的恒星的轨道半径大,故C错误;
D、两个恒星的动能之比为:
$\frac{{{E_{k1}}}}{{{E_{k2}}}}=\frac{{\frac{1}{2}{m_1}{{(ω{R_1})}^2}}}{{\frac{1}{2}{m_2}{{(ω{R_2})}^2}}}=\frac{{\frac{1}{2}{m_1}{{(ω\frac{m_2}{{{m_1}+{m_2}}}L)}^2}}}{{\frac{1}{2}{m_2}{{(ω\frac{m_1}{{{m_1}+{m_2}}}L)}^2}}}=\frac{m_2}{m_1}$
故质量大的恒星的动能小,质量小的恒星的动能大,故质量大的恒星的动能小于质量小的恒星的动能,故D正确;
故选:AD
点评 解决本题的关键知道双星模型靠相互间的万有引力提供向心力,角速度相等,周期相等,结合万有引力提供向心力进行分析判断.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
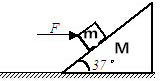 如图所示,质量为M=5kg的斜面体,放在水平地面上,斜面体倾角为37°,斜面上放有质量为m=3kg的物体,用水平力F推物体,两者一起沿水平地面匀速前进,斜面体与地面间的动摩擦因数μ=0.2,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,质量为M=5kg的斜面体,放在水平地面上,斜面体倾角为37°,斜面上放有质量为m=3kg的物体,用水平力F推物体,两者一起沿水平地面匀速前进,斜面体与地面间的动摩擦因数μ=0.2,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{{v}_{0}}{g}$ | B. | $\frac{2{v}_{0}}{g}$ | C. | $\frac{3{v}_{0}}{g}$ | D. | $\frac{4{v}_{0}}{g}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 第一个对亚里士多德的“力是维持物体运动的原因”提出质疑的科学家是牛顿 | |
| B. | 牛顿在给出万有引力公式F=$\frac{GMm}{{R}^{2}}$的同时也给出了引力常量G的数值 | |
| C. | 伽利略用实验的方法证实了重的物体比轻的物体下落得快 | |
| D. | 法拉第最先提出了场的概念,并最先用电场线形象地描绘电场 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 第1s内的平均速度是4m/s | |
| B. | 第1s内的位移是6m | |
| C. | 第2s内的位移是4m | |
| D. | 如果质点的质量m=1kg,则质点所受的合外力大小为2N,方向与初速度方向相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 温度是分子平均动能的标志,物体温度升高,则物体的分子平均动能增大 | |
| B. | 布朗运动是指在显微镜下观察到的组成悬浮颗粒的固体分子的无规则运动 | |
| C. | 气体的温度每升高1K所吸收的热量与气体经历的过程有关 | |
| D. | 一定质量的理想气体,若气体的压强和体积都不变,其内能也一定不变 | |
| E. | 当分子间的距离大于平衡位置的间距r0时,分子间的距离越大,分子势能越小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com