
科目: 来源: 题型:
 在绕地球做匀速圆周运动的卫星实验仓内,使一质量为m=1.0×
在绕地球做匀速圆周运动的卫星实验仓内,使一质量为m=1.0×![]() kg,带电量为Q=-4.0×
kg,带电量为Q=-4.0×![]() C的小球,以初速度
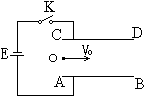
C的小球,以初速度![]() =10m/s,从相距为2d,长度5d的两平行金属板左 侧中点,沿平行于极板方向射入,如图所示.求:
=10m/s,从相距为2d,长度5d的两平行金属板左 侧中点,沿平行于极板方向射入,如图所示.求:
(1)为使小球恰能从AB极板的边缘B点射出,电源电动势E为多大?
(2)断开电源并使极板间电场强度为零,再在极板间加一垂直于纸面方向的匀强磁场,若d=10cm,为使小球恰能从CD极板的边缘D点射出,所加磁场的磁感强度B为多大?方向如何?
查看答案和解析>>
科目: 来源: 题型:
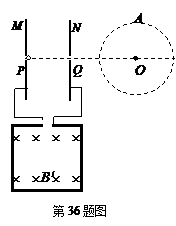
如图所示,一对平行放置的金属板M、N的中心各有一小孔P、Q,PQ连线垂直金属板;N板右侧的圆形区域A内分布有方向垂直于纸面向外的匀强磁场,磁感应强度大小为B,圆半径为r,且圆心O在PQ的延长线上,两平行金属板与匝数为n,边长为a的正方形线圈相连,现有垂直于线圈平面均匀增大的磁场,磁感应强度变化率为![]() ,一质量为m、电量为q的带负电粒子(重力不计),初速度为零,从P点进入两板间,求:
,一质量为m、电量为q的带负电粒子(重力不计),初速度为零,从P点进入两板间,求:
(1)两平行板之间的电势差
(2)粒子从Q点射出时的速度
(3)带电粒子通过该圆形磁场的偏转角θ
查看答案和解析>>
科目: 来源: 题型:
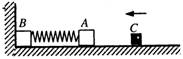
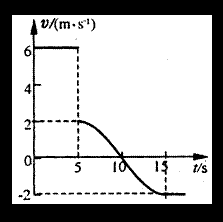
如图所示,物体A、B的质量分别是4kg和8kg,由轻弹簧相连接,放在光滑的水平面上,物体B左侧与竖直墙壁相接触,另有一个物体C水平向左运动,在t=5s时与物体A相碰,并立即与A有相同的速度,一起向左运动。物块C的速度一时间图象如图所示。
(1)求物块的质量。
(2)弹簧压缩具有的最大弹性势能。
(3)在5s到10s的时间内墙壁对物体B的作用力的功。
(4)在5s到15s的时间内墙壁对物体B的作用力的冲量。
查看答案和解析>>
科目: 来源: 题型:
一根不可伸长的细绳围成一个正方形,正方形的四个顶点分别连接着一个质量为m的质点A、B、C、D,正方形中心处有一质量M=2m的质点E,它们都静止在光滑水平面上。今使质点E以初速v0沿水平对角线方向运动,与质点C做完全非弹性碰撞。求:
(1)碰撞后细绳围成的正方形尚未被破坏的瞬时,各质点运动的速度,
(2)在以后运动过程中B、D两质点第一次相撞时的相对速度。
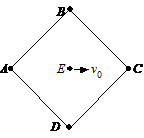
查看答案和解析>>
科目: 来源: 题型:
如图所示,水平放置的两块长直平行金属板a、b相距d=0.10m,a、b间的电场强度为E=5.0×105N/C,b板下方整个空间存在着磁感应强度大小为B=6.0T、方向垂直纸面向里的匀强磁场.今有一质量为m=4.8×10-25kg、电荷量为q=1.6×10-18C的带正电的粒子(不计重力),从贴近a板的左端以v0 =1.0×106m/s的初速度水平射入匀强电场,刚好从狭缝P处穿过b板而垂直进入匀强磁场,最后粒子回到b板的Q处(图中未画出).求P、Q之间的距离L.

查看答案和解析>>
科目: 来源: 题型:
如图所示,AB是半径为R的1/4光滑圆弧轨道。B点的切线在水平方向,且B点离水平地面高为h,有一物体(可视为质点)从A点静止开始滑下,重力加速度为g。求:
(1)物体运动到B点时的速度大小;
(2)物体到达B点时的加速度a1及刚离开B点时的加速度a2;
(3)物体落地点到B点的距离s 。

查看答案和解析>>
科目: 来源: 题型:
如图所示,一个质量为m,带电量为+q的粒子以速度v0从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从点b处穿过x轴,速度方向与x轴正方向的夹角为300.粒子的重力不计,试求:
(1)圆形匀强磁场区域的最小面积.
(2)粒子在磁场中运动的时间.
(3)b到O的距离.

查看答案和解析>>
科目: 来源: 题型:
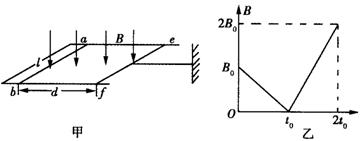
如图甲所示,电阻不计、间隔距为l的平行长直金属导轨置于水平面内,阻值为R的导体棒ab固定连接在导轨左端,另一阻值也为R的导体棒ef垂直旋转在导轨上,ef与导轨接触良好并可在导轨上无摩擦移动。现有一根轻杆一端固定中ef中中断过程,另一端固定于墙上;轻杆与导轨保持平行,ef、ab两棒之间距离为d。若整个装置处于方向竖直向下的匀强磁场中,且从某一时刻开始,磁感应强度B随时间t按图乙所示的方式变化。
(1)求0 ~ t0时间内流过导体棒ef的电流大小和方向;
(2)求t0 ~ 2t0时间内导体棒ef产生的热量;
(3)分别写出0 ~ t0、t0 ~ 2t0时间内轻杆受力F随时间t 变化的函数关系式,求出2t0时刻轻杆受力F的大小和方向。
查看答案和解析>>
科目: 来源: 题型:
以下是一位同学做“探究形变与弹力的关系”的实验.
(1)下列的实验步骤是这位同学准备完成的,请你帮这位同学按操作的先后顺序,用字母排列出来是: .
A.以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连结起来.
B.记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0
C.将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺
D.依次在弹簧下端挂上1个、2个、3个、4个……钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码
E.以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式.
F.解释函数表达式中常数的物理意义.
(2)下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据:
| 弹力(F/N) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| 弹簧原来长度(L0/cm) | 15 | 15 | 15 | 15 | 15 |
| 弹簧后来长度(L/cm) | 16.2 | 17.3 | 18.5 | 19.6 | 20.8 |
| 弹簧伸长量(x/cm) |
 ①算出每一次弹簧伸长量,并将结果填在上表的空格内
①算出每一次弹簧伸长量,并将结果填在上表的空格内
②在下图的坐标上作出F-x图线.
③写出曲线的函数表达式(x用cm作单位):
查看答案和解析>>
科目: 来源: 题型:
 如下图所示,半径为R=10cm的匀强磁场区域边界跟Y轴相切于坐标原点O,磁感强度B=0.322T,方向垂直纸面向里,在O处有一放射源S,可沿纸面向各个方向射出速率为V=3.2×
如下图所示,半径为R=10cm的匀强磁场区域边界跟Y轴相切于坐标原点O,磁感强度B=0.322T,方向垂直纸面向里,在O处有一放射源S,可沿纸面向各个方向射出速率为V=3.2×![]() 的α粒子.已知α粒子质量m=6.4×
的α粒子.已知α粒子质量m=6.4×![]() ,电量q=3.2×
,电量q=3.2×![]() .
.
(1)画出α粒子通过磁场空间做圆周运动的圆心点的轨迹.
(2)求出α粒子通过空间的最大偏转角![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com