
1. sin30°的值是 ( ▲ )
A.1 B. C. D.
2.已知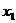 、
、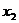 是一元二次方程
是一元二次方程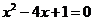 的两个根,则
的两个根,则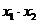 等于(▲ )
等于(▲ )
 A.
A. 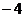 B.
B. 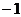 C. 1 D.
4
C. 1 D.
4
3. 下列一元二次方程中,无实数根的方程是( ▲ )
A. 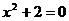 B.
B.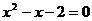 C.
C. 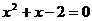 D.
D.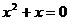
4.若两个相似多边形的面积之比为1:4,则它们的周长之比为( ▲ )
|
|
A. |
1:4 |
B. |
1:2 |
C. |
2:1 |
D. |
4:1 |
5.下列说法正确的是( ▲ )
A.经过三点可以作一个圆 B.三角形的外心到这个三角形的三边距离相等
C.等弧所对的圆心角相等 D.相等的圆心角所对的弧相等
6.已知⊙O的半径是6cm,点O到同一平面内直线L的距离为5cm,则直线L与⊙O的位置关系是( ▲ )
A.相交 B.相切
 C.相离
D.无法判断
C.相离
D.无法判断
7. 如图,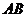 是⊙0的直径,点
是⊙0的直径,点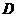 在
在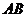 的延长线上,过点
的延长线上,过点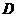 作⊙0的切线,切点为
作⊙0的切线,切点为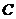 ,若
,若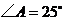 ,则
,则 (
)
(
)
A. 60° B.65° C.50° D.40°
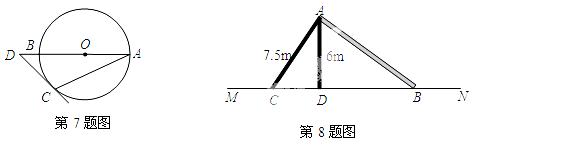
8. 如图,在平地MN上用一块10m长的木板AB搭了一个斜坡,两根支柱AC=7.5m,AD=6m,其中AC⊥AB,AD⊥MN,则斜坡AB的坡度是( ▲ )
A. 3:5 B. 4:5 C. 3:4 D. 4:3
9. 如图,点D为△ABC的边AB上的一点,连结CD,过点B作BE//AC交CD的延长线于点E,且∠ACD=∠DBC, ,AB=10,则AC的长为( ▲
).
,AB=10,则AC的长为( ▲
).
 A.
A. 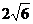 B.
B.
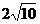 C.
6 D.
C.
6 D.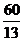
|
10. 已知等腰梯形ABCD中,AD∥BC,∠B=45°,AD=2-2.动点P在折线BA-AD-DC上移动,若存在∠BPC=120°,且这样的P点恰好出现3次,则梯形ABCD的面积是( ▲ )
A.2-1 B.2-2 C.2 D.2+1
11. 在1:500000的无锡市地图上,新建的地铁线估计长4.5cm,那么等地铁造好后实际长约为 ▲ 千米。
12. 在相同时刻的物高与影长成比例,如果高为1.5m的测杆的影长为2.5m,那么影长为30 m的旗杆的高是 ▲ m.
13. 网民小李的QQ群里共有若干个好友,每个好友都分别给群里其他好友发送了一条消息,这样共有90条消息,设小李的QQ群里共有好友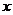 个,可列方程为:
▲
.
个,可列方程为:
▲
.
14.用计算器计算: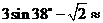 (精确到0.01).
(精确到0.01).
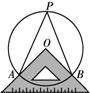
15. 如图,将三角板的直角顶点放在⊙O的圆心上,两条直角边分别交⊙O于A、B两点,点P在优弧AB上,且与点A、B不重合,连结PA、PB.则∠APB的大小为 ▲ °
|
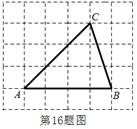
16.如图,将 放在每个小正方形的边长为1的网格中,点
放在每个小正方形的边长为1的网格中,点 、
、 、
、 均落在格点上,用一个圆面去覆盖
均落在格点上,用一个圆面去覆盖 ,能够完全覆盖这个三角形的最小
,能够完全覆盖这个三角形的最小 圆面的面积是 ▲ .
圆面的面积是 ▲ .
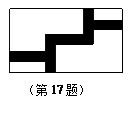
17.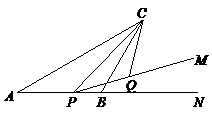 如图,在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪.要使草坪的面积为540米,则道路的宽为
▲ 米.
如图,在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪.要使草坪的面积为540米,则道路的宽为
▲ 米.
 |
|||
|
|||
18.如图,△ABC中,AC=10,∠BAC=30°,点P是射线AB上的一个动点,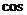 ∠CPM=
∠CPM= ,点Q是射线PM上的一个动点.则CQ长度的最小
,点Q是射线PM上的一个动点.则CQ长度的最小 值是 ▲ .
值是 ▲ .
1 9.解方程(每小题4分,共8分)
9.解方程(每小题4分,共8分)
(1) x2-4x+2=0; (2)3x(x-3) =2(x-3).
20. (本题满分8分)已知关于x的方程(a-1)x2-4x-1+2a=0的一个根为x=3.
(1)求a的值及方程的另一个根;
(2)如果一个三角形的三条边长都是这个方程的根,求这个三角 形的周长.
形的周长.
21. (本题满分6分)如图,矩形ABCD中,E为BC上 一点,DF⊥AE于点F。
一点,DF⊥AE于点F。
(1)求证:△ABE∽△DFA; (2)若AB=6,AD=12,BE=8,求DF的长。

22.(本题满分8分)
如图10,在平面直角坐标系中,△AOB的顶点坐标分别为A (2,1)、O(0,0)、B(1,-2).
(2,1)、O(0,0)、B(1,-2).
(1)P(a,b)是△AOB的边AB上一点,△AOB经平移后点P的对应点为P2(a-3, b+1),请画出上述平移后的△A1O1B1,并写出点A1的坐标;
(2)以点O为位似中心,在y轴的右侧画出△AOB的一个位似△A2OB2,使它与
△AOB的相似比为2:1,并分别写出点A、P的对应点A2、P2的坐标;
(3)判断△A2OB2与△A1O1B1能否是关于某一点Q为位似中心的位似图形,若是,请在图10中标出位似中心Q,并写出点Q的坐标.

23.(本题满分8分)
电动自动车已成为市民日常出行的首选工具.据某市某品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月份销售216辆.
(1)求该品牌电动自行车销售量的月均增长率;
(2)若该品牌电动自行车的进价为2300元,售价为2800元,则该经销商1至3月共盈利多少元?
24.(本题满分6分)
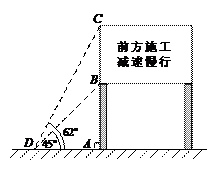
进入3月份,我市“两横三纵”快速路系统全线开工.为缓解市区内一些主要路段交通拥挤的现状,交警部门在一些主要路口设立了如图所示的交通路况显示牌 .已知立杆AB的高度是3米,从地面上某处D点测得显示牌顶端C点和底端B点的仰角分别是62°和45°.求路况显示牌BC的高度.(精确到0.1米)
.已知立杆AB的高度是3米,从地面上某处D点测得显示牌顶端C点和底端B点的仰角分别是62°和45°.求路况显示牌BC的高度.(精确到0.1米)
 [参考数据:
[参考数据: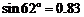 ,
,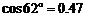 ,
,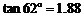 ]
]
25.(本题满分8分)
如图,有一长方形的仓库,一边长为5米.现要将它改建为简易住房,改建
后的住房分为客厅、卧室和卫生间三部分,其中客厅和卧室都为正方形,且卧室的面积大于卫生间的面积.若改建后卫生间的面积为6平方米,试求长方形仓库另一边的长.

26.(本题满分10分)
如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(-2,0)、B(4,0)、C(0,2).
(1)请用尺规作出△ABC的外接圆⊙P(保留作图痕迹,不写作法);
(2) 求出(1)中外接圆圆心P的坐标;
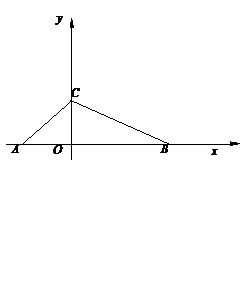 (3)⊙P上是否存在一点Q,使得△QBC与△AOC相似?如果存在,请求出点Q 坐标;如果不存在,请说明理由.
(3)⊙P上是否存在一点Q,使得△QBC与△AOC相似?如果存在,请求出点Q 坐标;如果不存在,请说明理由.
27.(本题满分10分)
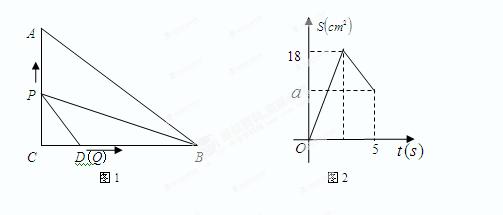
如图1,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点D是BC上一定点.动点P从C出发,以2cm/s的速度沿C→A→B方向运动,动点Q从D出发,以1cm/s的速度沿D→B方向运动.点P出发5 s后,点Q才开始出发,且当一个点达到B时,另一个点随之停止. 图2是当 时△BPQ的面积S( cm2)与点P的运动时间t(s)的函数图象.
时△BPQ的面积S( cm2)与点P的运动时间t(s)的函数图象.
(1)CD =
, 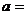 ;
;
(2)当点P在边AB上时,t为何值时,使得△BPQ与△ABC为相似?
(3)运动过程中,求出当△BPQ是以BP为腰的等腰三角形时t的值.
28.(本题满分12分)
如图,在平面直角坐标系中,矩形OAB C的四个顶点坐标分别为O(0,0),A(4,0),B(4,3),C(0,3),G是对角线AC的中点,动直线MN平行于AC且交矩形OABC的一组邻边于E、F,交y轴、x轴于M、N.设点M的坐标为(0,t),△EFG的面积为S.
C的四个顶点坐标分别为O(0,0),A(4,0),B(4,3),C(0,3),G是对角线AC的中点,动直线MN平行于AC且交矩形OABC的一组邻边于E、F,交y轴、x轴于M、N.设点M的坐标为(0,t),△EFG的面积为S.
(1)求S与t的函数关系式;
(2)当△EFG为直角三角形时,求t的值;
(3)当点G关于直线EF的对称点G′ 恰好落在矩形OABC的一条边所在直线上时,直接写出t的值.

江苏省宜兴市屺亭中学2015届九年级数学上学期期中试题参考答案
初三数学参考答案
 那么三角形的周长是3或9;
…………………5分
那么三角形的周长是3或9;
…………………5分
②仅有两边相等,因为1+1=2<3,所以三角形的边长只能为3,3,1.
那么三角形的周长是7.------------7分
由①、②知,三角形的周长可以是3,或7,或9. ---------- 8分
21. (1)∵四边形ABCD是矩形, ∴AD∥BC,∠B=90°, ∴∠AEB=∠DAE,
∵DF⊥AE∴∠ADF=∠EAB∴△ABE∽△DFA; --------3分
(2)在直角三角形ABE中,由勾股定理,得,AE=10,
因为△ABE∽△DFA;所以AB/DF=AE/DA,即6/DF=10/12
解得DF=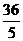 ------6分
------6分
22. (1)如图1,A1(-1,2) …………………2分
(2)如图1,A2(4,2) ,P2 (2a,2b) …………………5分
(3)如图1,△A2OB2与△A1O1B1是关于点Q为位似中心的位似图形.
 Q(-6,2)
…………………8分
Q(-6,2)
…………………8分

23. 解:(1)设该品牌电动自行车销售量的月均增长率为x,
根据题意列方程:150(1+x)2=216,---------3分
解得x1=-220%(不合题意,舍去),x2=20%.------4分
答:求该品牌电动自行车销售量的月均增长率20%.----5分
(2)二月份的销量是:150×(1+20%)=180(辆).----6分
所以该经销商1至3月共盈利:(2800-2300)×(150+180+216)=500×546=273000(元).-------8分
24. 在Rt△ADB中,∵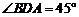 , ∴
, ∴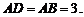 ------2分
------2分
在Rt△ADC中,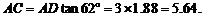 --
-- -----4分
-----4分
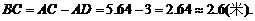 -------5分
-------5分
答:路况显示牌BC的高度是2.6米 -------6分
25. 解:设长方形的 另一边的长为x米
…………………………1分
另一边的长为x米
…………………………1分
由题意得:(x -5)[5 -(x -5)]=6, …………………………4分
整理得:x2 -15x+56=0, ……………………(5分
解之得:x1=7,x2=8 , ……………………………6分
因为当x=7时,卧室 面积小于卫生间面积,所以舍去.……7分
面积小于卫生间面积,所以舍去.……7分
答:长方形的另一边的长为8米.…………………8分
26. (1)作图略;----3分
(2)点P坐标为(1,-1). ………………………6分
(3)(-2,-2),(2,-4)---------10分(注:直接给出答案得一半分)
27.(1)CD=2,a=10.8---------2分
(2)4.25秒或6秒---------6分
(3)5秒或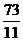 秒---------10分
秒---------10分
28. (1) 当0<t <3时,S=- t 2+2t ------2分
当3<t <6时S=- t 2+6t-12 --------4分
(2)①若∠EFG=90°,则点F在线段AB上
t=
②若∠EGF=90°且点F在线段OA上t=
若∠EGF=90°且点F在线段AB上t=
③若∠FEG=90°,则点F在线段AB上t= --------8分
(3)t1= ,t2= ,t3= ,t4= --------12分