
1、有两个角互余的三角形是直角三角形。
2、勾股定理逆定理
1、直角三角形两锐角互余.
2、直角三角形中30°所对的直角边等于斜边的一半.
3、直角三角形中,斜边的中线等于斜边的一半;
4、勾股定理:直角三角形两直角边a,b的平方和等于斜边c的平方,即a2+b2=c2.5.直角三角形两直角边a,b的平方和等于斜边c的平方,即a2+b2=c2.
由广勾股定理我们可以自然地推导出三角形三边关系对于角的影响.在△ABC中,
(1)若c2=a2+b2,则∠C=90°;
(2)若c2<a2+b2,则∠C<90°;
(3)若c2>a2+b2,则∠C>90°.
勾股定理及广勾股定理深刻地揭示了三角形内部的边角关系,因此在解决三角形(及多边形)的问题中有着广泛的应用.
5、勾股定理逆定理:如果三角形三边长a,b,c有下面关系:a2+b2=c2那么这个三角形是直角三角形.
6、勾股数的定义:如果三个正整数a、b、c满足等式a2+b2=c2,那么这三个正整数a、b、c叫做一组勾股数。简单的勾股数有:3,4,5; 5,12,13; 7,24,25; 8,15,17; 9,40,41。
[典例精析]
◆例1:在△ABC中,∠BAD=90°,AB=3,BC=5,现将它们折叠,使B点与C点重合,求折痕DE的长。
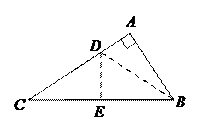
[巩固]
1、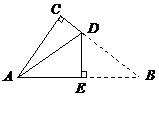 如图是一张直角三角形的纸片,两直角边AC=6 cm、BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6 cm、BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm B.5 cm C.6 cm D.10 cm
2、四边形ABCD中,∠DAB=60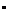 ,∠B=∠D=90°,BC=1,CD=2;求对角线AC的长?
,∠B=∠D=90°,BC=1,CD=2;求对角线AC的长?

◆例2:如图所示.已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.求证:AB2=2FG2.

[巩固]已知△ABC中,∠A=90°,M是BC的中点,E,F分别在AB,AC上,ME⊥MF
求证:EF2=BE2+CF2

◆例3:已知正方形ABCD的边长为1,正方形EFGH内接于ABCD,AE=a,AF=b,且SEFGH=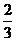
 求:
求: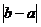 的值
的值
◆例4:已知:P为△ABC内一点,且PA=3,PB=4,PC=5,求∠APB的度数

 [巩固]如图,四边形ABCD中,AC⊥BD,AC与BD交于O点,AB=15,BC=40,CD=50,则AD=________.
[巩固]如图,四边形ABCD中,AC⊥BD,AC与BD交于O点,AB=15,BC=40,CD=50,则AD=________.
◆例5:一个直角三角形的三条边长均为整数,它的一条直角边的长为15,那么它的另一条直角边的长有_______种可能,其中最大的值是______.
[拓展]是否存在这样的直角三角形,它的两条直角边长为整数,且它的周长与面积的数值相等?若存在,求出它的各边长;若不存在,说明理由。
[课外练习]
1、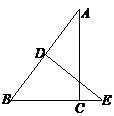 如图,在RtΔABC中,∠ACB=90°BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
如图,在RtΔABC中,∠ACB=90°BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
A.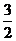 B.
B.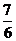 C.
C.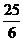 D.2
D.2
2、如图,等腰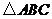 中,
中,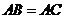 ,
,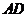 是底边上的高,若
是底边上的高,若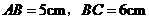 ,
,
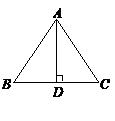 则
则 cm.
cm.
3、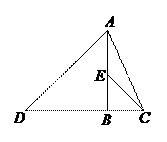 已知AB⊥CD,△ABD,△BCE都是等腰三角形,CD=8,BE=3,则AC的长等于( )
已知AB⊥CD,△ABD,△BCE都是等腰三角形,CD=8,BE=3,则AC的长等于( )
A.8
B.5 C.3 D.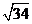
4、如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是
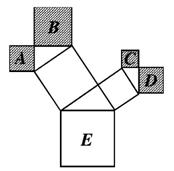 A.13
B.26 C.47 D.94
A.13
B.26 C.47 D.94
5、如图,在矩形ABCD中,在DC上存在一点E,沿直线AE折叠,使点D恰好落在BC边上,设此 点为F,若△ABF的面积为30cm2,那么折叠的△AED的面积为_______.
点为F,若△ABF的面积为30cm2,那么折叠的△AED的面积为_______.
