
(1)若集合A={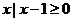 },B={
},B={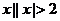 },则集合
},则集合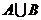 等于( ).
等于( ).
(A) {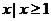 } (B)
{
} (B)
{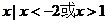 }
}
(C) { 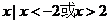 }
(D) {
}
(D) {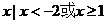 }
}
 (2)已知实数x,y满足约束条件
(2)已知实数x,y满足约束条件 ,则
,则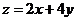 的最小值是( ).
的最小值是( ).
(A) 5 (B) -6
(C) 10 (D) -l0
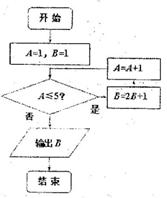
(3)若某程序框图如图所示,则该程序运行后输出的B等于( ).
(A) 7 (B) 15
(C) 31 (D) 63
(4)已知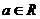 且
且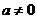 ,则“
,则“ ”是“
”是“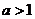 ”的( )
”的( )
(A) 充分不必要条件 (B) 必要不充分条件
(C) 充要条件 (D) 既不充分也不必要条件
(5)过点A(-1,0),斜率为k的直线,被圆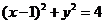 截得的弦长为2
截得的弦长为2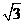 ,则k的值为( )。
,则k的值为( )。
(A) 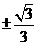 (B)
(B)
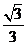
(C) 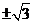 (D)
(D)
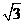
(6)函数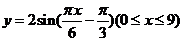 的最大值与最小值之和为( )。
的最大值与最小值之和为( )。
(A) 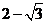 (B)
0
(B)
0
(C) 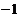 (D)
(D)
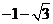
(7)设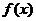 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当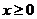 时,
时,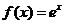 。若对任意的x
。若对任意的x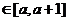 ,不等式
,不等式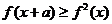 恒成立,则实数a的最大值是( )。
恒成立,则实数a的最大值是( )。
(A) 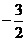 (B)
(B)
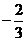
(C)  (D)
2
(D)
2
(8)设定义域为R的函数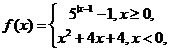 若关于x的方程
若关于x的方程 有7个不同的实数解,则m=( ).
有7个不同的实数解,则m=( ).
(A) 2 (B) 4或6
(C) 2或6 (D) 6
南开区2013-2014学年度第二学期高三年级总复习质量检测(一)
答题纸(文史类)
第Ⅱ卷
(9)若复数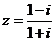 ,则
,则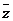 等于
.
等于
.
(10)平面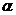 截球O的球面所得圆的半径为1,球心O到平面
截球O的球面所得圆的半径为1,球心O到平面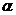 的距离为
的距离为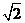 ,则此球的体积为 .
,则此球的体积为 .
 (11) 已知双曲线
(11) 已知双曲线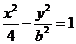 的右焦点与抛物线
的右焦点与抛物线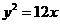 的焦点重合,则该双曲线的焦点到其渐近线的距离为 。
的焦点重合,则该双曲线的焦点到其渐近线的距离为 。
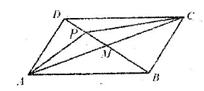
 (12)如图,平行四边形ABCD的两条对角线相交于点M,点P是MD的中点.若
(12)如图,平行四边形ABCD的两条对角线相交于点M,点P是MD的中点.若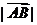 =2,
=2,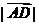 =1,且
=1,且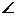 BAD=60o,则
BAD=60o,则
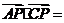 。
。
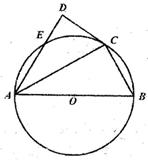
(13)已知AB为圆O的直径,AB=4,C为半圆上一点,过点C作圆O的切线CD,过点A作AD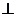 CD于D,交圆O于点E,DE=1,则BC的长为
。
CD于D,交圆O于点E,DE=1,则BC的长为
。
(14)已知a,b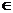 R,2a2-b2=1,则|2a-b|的最小值为 .
R,2a2-b2=1,则|2a-b|的最小值为 .
(15)(本小题满分13分)
城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求。某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟).
|
组别 |
一 |
二 |
三 |
四 |
五 |
|
候车时间 |
[0,5) |
[5,10) |
[10,15) |
[15,20) |
[20,25] |
|
人数 |
2 |
6 |
4 |
2 |
l |
(I)估计这60名乘客中候车时间少于10分钟的人数;
(II)若从上表第三、四组的6人中任选2人作进一步的调查.
①列出所有可能的结果;
②求抽到的两人恰好来自不同组的概率。
(16)(本小题满分13分)
在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=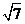 ,C=
,C=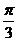
(I)若2sinA=3sinB,求a,b;
(II)若cosB=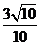 ,求sin2A的值,
,求sin2A的值,
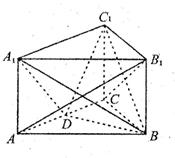 (17)(本小题满分13分)
(17)(本小题满分13分)
如图所示,在三棱柱ABC-A1B1C1中,侧棱A1A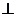 底面ABC,且底面是边长为2的正三角形,侧棱长为1,D是AC的中点.
底面ABC,且底面是边长为2的正三角形,侧棱长为1,D是AC的中点.
(I)求证:B1C//平面A1BD;
(II)求证:平面A1BD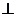 平面C1BD:
平面C1BD:
(III)求直线AB1与平面A1BD所成的角的正弦值.
(18)(本小题满分13分)
已知椭圆C: (a>b>0)的离心率为
(a>b>0)的离心率为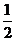 ,过右焦点F的直线l与C相交于A、B两点,当l的斜率为l时,坐标原点O到l的距离为
,过右焦点F的直线l与C相交于A、B两点,当l的斜率为l时,坐标原点O到l的距离为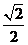 。
。
(I)求椭圆C的方程;
(II)若P,Q,M,N椭圆C上四点,已知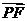 与
与 共线,
共线,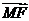 与
与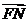 共线,且
共线,且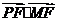 =0,求四边形PMQN面积的最小值.
=0,求四边形PMQN面积的最小值.
(19)(本小题满分14分)
己知各项均为正数的数列{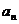 }满足
}满足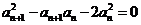 (
(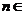 N*),且
N*),且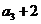 是
是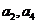 的等差中项。
的等差中项。
(I)求数列{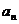 }的通项公式
}的通项公式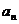 ;
;
(II)若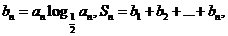 ,求
,求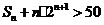 使成立的正整数n的最小值.
使成立的正整数n的最小值.
(20)(本小题满分14分)
设函数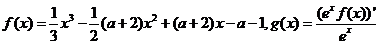 ,其中a>0.
,其中a>0.
(I)讨论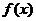 的单调性;
的单调性;
(II)设曲线y=g(x)在点(m,g(m)),(n,g(n))处的切线都过点(0,2)。证明:当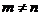 时,
时,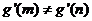 。
。