
1.直线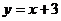 与
与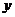 轴的交点坐标是( )
轴的交点坐标是( )
A.(0,3) B.(0,1) C.(3,O) D.(1,0)
2.如图,过点Q(0,3.5)的一次函数与正比例函数y=2x的图象相交于点P,能表示这个一次函数图象的方程是( )
A.3x-2y+3.5=0 B.3x-2y-3.5=0 C.3x-2y+7=0 D.3x+2y-7=0
3.
 如图,小球从点A运动到点B,速度v(米/秒)和时间t(秒)的函数关系式是v=2t.如果小球运动到点B时的速度为6米/秒,小球从点A到点B的时间是( ).
(A)1秒 (B)2秒 (C)3秒 (D)4秒
如图,小球从点A运动到点B,速度v(米/秒)和时间t(秒)的函数关系式是v=2t.如果小球运动到点B时的速度为6米/秒,小球从点A到点B的时间是( ).
(A)1秒 (B)2秒 (C)3秒 (D)4秒
4.一次函数y=-3x-2的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知四条直线 ,
, ,
,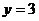 和
和 所围成的四边形的面积是12,则
所围成的四边形的面积是12,则 的值为( )
的值为( )
A.1或-2 B.2或-1 C.3 D.4
6.函数 ,
, .当
.当 时,则
时,则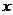 的范围是( )
的范围是( )
A..x<-1 B.-1<x<2 C.x<-1或x>2 D.x>2
7.若直线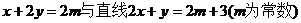 的交点在第四象限,则整数m的值为( )
的交点在第四象限,则整数m的值为( )
A.-3,-2,-1,0 B.-2,-1,0,1
C.-1,0,1,2 D.0,1,2,3
8.两直线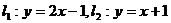 的交点坐标为( )
的交点坐标为( )
A.(-2,3) B.(2,-3) C.(-2,-3) D.(2,3)
9.已知函数y=kx的函数值随x的增大而增大,则函数的图像经过( )
A.第一、二象限 B. 第一、三象限 C.第二、三象限 D.第二、四象限
10. 一次函数
一次函数 的图象如图所示,当
的图象如图所示,当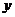 <0时,x的取值范围是( )
<0时,x的取值范围是( )
(A)x<0 (B)x>0
(C)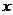 <2 (D)x>2
<2 (D)x>2
11.对于函数y=k x(k是常数,k≠0)的图象,下列说法不正确的是( )
x(k是常数,k≠0)的图象,下列说法不正确的是( )
A.是一条直线
B.过点( ,k)
,k)
C.经过一、三象限或二、四象限 D.y随着x增大而增大
12. (
( 、
、 (
( 是一次函数
是一次函数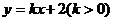 图像上的不同的两点,若t=
图像上的不同的两点,若t= 则( )
则( )
A .  B.
B.
 C.
C.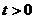 D.
D. 
1.如果正比例函数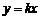 的图象经过点(1,-2),那么k 的值等于 .
的图象经过点(1,-2),那么k 的值等于 .
2.已知一次函数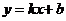 的图象交
的图象交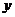 轴于正半轴,且
轴于正半轴,且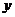 随
随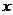 的增大而减小,请写出符合上述条件的一个解析式: .
的增大而减小,请写出符合上述条件的一个解析式: .
3.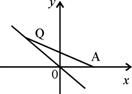
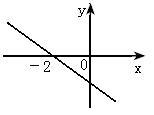
 已知一次函数
已知一次函数 的图象如图所示,当
的图象如图所示,当 时,
时,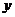 的取值范围是 .
的取值范围是 .
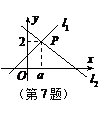
第4题 第5题 第9题
4.一次函数 (
( 为常数且
为常数且 )的图象如图所示,则使
)的图象如图所示,则使 成立的
成立的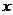 的取值范围为 .
的取值范围为 .
5.将直线 y = 2 x ─ 4 向上平移5个单位后,所得直线的表达式是______________.
6.直线y = 2x +6与两坐标轴围成的三角形面积是
7.如图,直线 :
: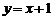 与直线
与直线 :
: 相交于点P(
相交于点P(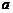 ,2),则关于
,2),则关于 的不等式
的不等式 ≥
≥ 的解集为 .
的解集为 .
8.已知一次函数 与
与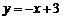 的图象交于点
的图象交于点 ,则点
,则点 的坐标为 .
的坐标为 .
9.如图,点Q在直线y=-x上运动,点A的坐标为(1,0),当线段AQ最短时,点Q的坐标为___________。
10.直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是x=______
11.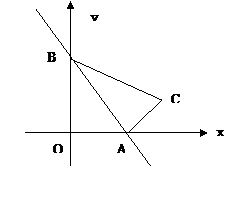 如图,直线1:
如图,直线1: 与
与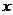 轴、
轴、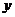 轴分别相交于点
轴分别相交于点 、
、 ,△AOB与△ACB关于直线
,△AOB与△ACB关于直线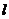 对称,则点C的坐标为
对称,则点C的坐标为
12.在一次函数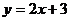 中,
中,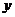 随
随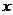 的增大而 (填“增大”或“减小”),当
的增大而 (填“增大”或“减小”),当 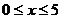 时,y的最小值为 .
时,y的最小值为 .
13.在平面直角坐标系中,将直线 向下平移4个单位长度后。所得直线的解析式为
.
向下平移4个单位长度后。所得直线的解析式为
.
14.将函数y=-6x的图象 向上平移5个单位得直线
向上平移5个单位得直线 ,则直线
,则直线 与坐标轴围成的三角形面积为 .
与坐标轴围成的三角形面积为 .
1.已知直线经过点(1,2)和点(3,0),求这条直线的解析式.
2.在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
(1)求函数y=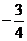 x+3的坐标三角形的三条边长;
x+3的坐标三角形的三条边长;
(2)若函数y=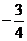 x+b(b为常数)的坐标三角形周长为16, 求此三角形面积.
x+b(b为常数)的坐标三角形周长为16, 求此三角形面积.
3.问题探究:
(1)请你在图①中作一条直线,使它将矩形ABCD分成面积相等的两部分;
(2)如图②,点M是矩形ABCD内一定点,请你在图②中过点M作一条直线,使它将矩形ABCD分成面积相等的两部分。
问题解决
(3)如图③,在平面直角坐标系中,直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图,其中CD//OB,OB=6,BC=4,CD=4。开发区综合服务管理委员会(其占地面积不计)设在点P(4,2)处,为了方便驻区单位,准备过点P修一条笔直的道路(路的宽度不计),并且使这条路所在的直线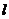 将直角梯形OBCD分成面积相等的两部分,你认为直线
将直角梯形OBCD分成面积相等的两部分,你认为直线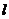 是否存在?若存在,求出直线
是否存在?若存在,求出直线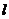 的表达式;若不存在,请说明理由。
的表达式;若不存在,请说明理由。
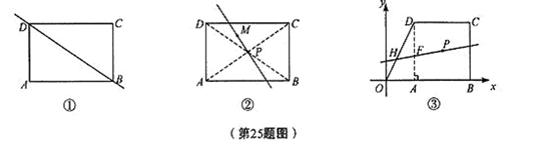
4.如图,已知:一次函数: 的图像与反比例函数:
的图像与反比例函数:
 的图像分别交于A、B两点,点M是一次函数图像在第一象限部分上的任意一点,过M分别向x轴、y轴作垂线,垂足分别为M1、M2,设矩形MM1OM2的面积为S1;点N为反比例函数图像上任意一点,过N分别向x轴、y轴作垂线,垂足分别为N1、N2,设矩形NN1ON2的面积为S2;
的图像分别交于A、B两点,点M是一次函数图像在第一象限部分上的任意一点,过M分别向x轴、y轴作垂线,垂足分别为M1、M2,设矩形MM1OM2的面积为S1;点N为反比例函数图像上任意一点,过N分别向x轴、y轴作垂线,垂足分别为N1、N2,设矩形NN1ON2的面积为S2;
 (1)若设点M的坐标为(x,y),请写出S1关于x的函数表达式,并求x取何值时,S1的最大值;
(1)若设点M的坐标为(x,y),请写出S1关于x的函数表达式,并求x取何值时,S1的最大值;
(2)观察图形,通过确定x的取值,试比较S1、S2的大小.
5.在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为 、
、 (km),
(km), 、
、 与x的函数关系如图所示.
与x的函数关系如图所示.
(1)填空:A、C两港口间的距离为 km, ;
;
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
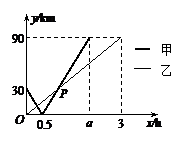 (3)若两船的距离不超过10 km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.
(3)若两船的距离不超过10 km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.
6.如图,直线 与
与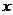 轴、
轴、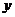 轴分别交与
轴分别交与 两点,
两点, .
.
(1)
求 点的坐标和
点的坐标和 的值;
的值;
(2)
若点 是第一象限内的直线
是第一象限内的直线 上的一个动点.当点
上的一个动点.当点 运动过程中,试写出△AOB的面积
运动过程中,试写出△AOB的面积 与
与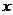 的函数关系式;
的函数关系式;
(3) 探索:
①当点A运动到什么位置时,△AOB的面积是 ;
;
②在①成立的情况下,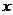 轴上是否存在一点
轴上是否存在一点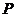 ,使△
,使△ 是等腰三角形.若存在,请写出满足条件的所有
是等腰三角形.若存在,请写出满足条件的所有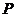 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
