
1.如果反比例函数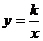 (
(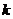 ≠0)的图象经过点(-2,1
≠0)的图象经过点(-2,1 ),那么
),那么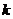 的值为( )
的值为( )
A.
2 B. -2 C. -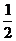 D.
D. 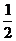
2.抛物线y=2(x﹣3)2﹣1的对称轴是直线 ( )
A、x=-1 B、x=2 C、x=3 D、x=﹣3
3. 如图,小正方形的边长 为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
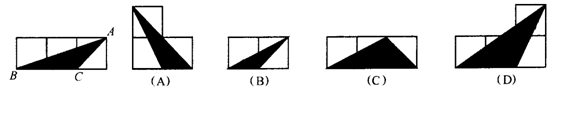
4.将直径为60 cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为( )
A.10 cm B.30 cm C.40 cm D.300 cm
5.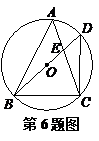 把抛物线y=x2+2x+5的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是( )
把抛物线y=x2+2x+5的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是( )
A.y= x2-2x+5 B. y= x2+8x+18 C. y=x2-4x+6 D.y= x2+2x+3
6.如图,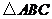 内接于圆
内接于圆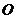 ,
,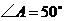 ,
,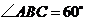 ,圆
,圆
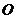 的
的
直径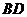 交
交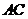 于点
于点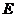 ,连结
,连结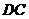 ,则
,则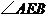 等于( )
等于( )
A.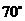 B.
B.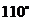 C.
C.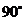 D.
D.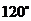
7. 二次函数
二次函数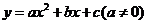 的图象如图4所示则下列说法不正
的图象如图4所示则下列说法不正 确的
确的
是( )
A.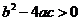 B.
B.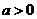 C.
C.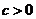 D.
D. 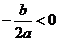
8.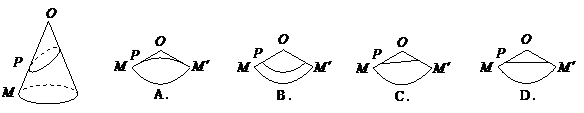 已知
已知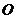 为圆锥的顶点,
为圆锥的顶点,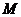 为圆锥底面上一点,点
为圆锥底面上一点,点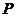 在
在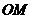 上.一只蜗牛从
上.一只蜗牛从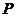 点出发,绕圆锥侧面爬行,回到
点出发,绕圆锥侧面爬行,回到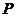 点时所爬过的最短路线的痕迹如右图所示.若沿
点时所爬过的最短路线的痕迹如右图所示.若沿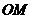 将圆锥侧面剪开并展开,所得侧面展开图是( )
将圆锥侧面剪开并展开,所得侧面展开图是( )
9.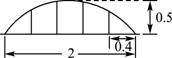 某公园草坪的防护栏是由100段形状相同的抛物线形组成的.为了牢固起见,每段护栏需要间距0.4 m加设一根不锈钢的支柱,防护栏的最高点距底部0.5 m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
某公园草坪的防护栏是由100段形状相同的抛物线形组成的.为了牢固起见,每段护栏需要间距0.4 m加设一根不锈钢的支柱,防护栏的最高点距底部0.5 m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
A.1.6 m B.100 m  C.160 m D.200 m
C.160 m D.200 m
10.抛物线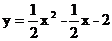 与直线
与直线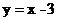 交于A,B两点(A在B的左侧)动点P从A出发先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到B,若使得点P的运动的总路程最短,则点P的总路程长为( )
交于A,B两点(A在B的左侧)动点P从A出发先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到B,若使得点P的运动的总路程最短,则点P的总路程长为( )
 A
A 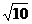
 B
B
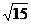 C
C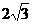 D
D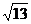
11.数3和12的比例中项是
 。
。
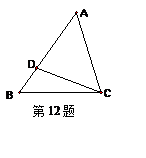
12.如图,D是△ABC中边AB上一点.请添加一个条件: ,
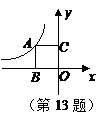 使 △ACD∽△ABC.
使 △ACD∽△ABC.
13.如图,点A是反比例函数图象上的一点,过点A分别向x轴、y轴作垂线,
若矩形ABOC的面积为3,则这个反比例函数的关系式是 .
14.一个扇形的弧长为10πcm,面积为120πcm2,则该扇形的圆心角
是 。
15.小芳在打网球时,为使球恰好能过网(网高为0.8m )且落在对方区域离网 5m的位置处,已知她击球的高度是2.4m,则她应站在离网的 m处。
16.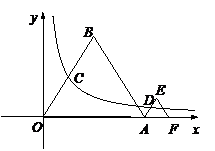 如图,等边△OAB和等
如图,等边△OAB和等 边△AFE的一边都在x轴上,双曲线
边△AFE的一边都在x轴上,双曲线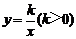 经过边OB的中点C
经过边OB的中点C
和 AE的中点D, 已知等边△OAB的边长为4.,
AE的中点D, 已知等边△OAB的边长为4.,
则E的坐标
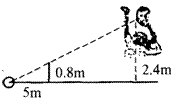
第15题图 第16题图
17.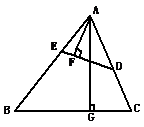 (8分)如图,D、E分别是AC,AB上的点,∠ADE=∠B,AG⊥BC于点G,AF⊥DE于点F.若AD=3,AB=5,求:
(8分)如图,D、E分别是AC,AB上的点,∠ADE=∠B,AG⊥BC于点G,AF⊥DE于点F.若AD=3,AB=5,求:
(1);
(2)△ADE与△ABC的周长之比;
(3)△ADE与△ABC的面积之比.
18.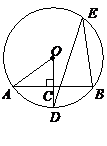 (10分).如图所示,
(10分).如图所示,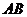 是⊙O的一条弦,
是⊙O的一条弦,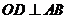 ,垂足为
,垂足为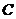 ,交⊙O于点
,交⊙O于点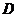 ,
,
点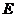 在⊙O上.
在⊙O上.
(1)若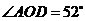 ,求
,求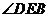 的度数;
的度数;
(2)若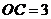
 ,
,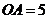 ,求
,求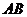 的长.
的长.
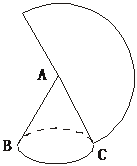
19.(10分)如图,一个圆锥的高为3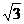 cm,侧面展开图是半圆.求:
cm,侧面展开图是半圆.求:
(1)圆锥的母线长与底面半径之比;
(2)圆锥的侧面积
20.(本题10分)
如图,一次函数y =kx+b的图象与反比例函数 图象交于A(-2,1)、B(1,n)两点。
图象交于A(-2,1)、B(1,n)两点。
(1)求反比例函数和一次函数的解析式;
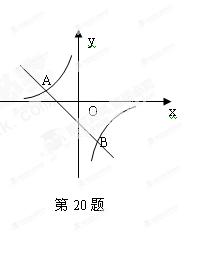 (2)根据图象写出当1<x<4时,反比例函数y的取值范围。
(2)根据图象写出当1<x<4时,反比例函数y的取值范围。
21.(本题10分)
已知二次函数的图像经过点(0,-3),且顶点坐标为(1,-4)。
(1)求该二次函数的解析式.
(2)当x为何值时,y随x的增大而增大?x为何值时,y随X的增大而减小?
(3)当x为何值时,y>0
22. (10分)如图,在⊙M中,弦AB所对的圆心角为
(10分)如图,在⊙M中,弦AB所对的圆心角为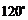 ,已知圆的半径为1cm,
,已知圆的半径为1cm,
并建立如图所示的直角坐标系.
(1)求圆心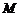 的坐标;
的坐标;
(2)求经过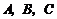 三点的抛物线的解析式;
三点的抛物线的解析式;
(3)点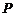 是⊙M上的一个动点,当
是⊙M上的一个动点,当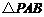 为Rt△时,
为Rt△时,
求点p的坐标。
23.(12分)某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10 万元时,可全部租出.每间的年租金每增加5000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5
000元.
万元时,可全部租出.每间的年租金每增加5000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5
000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)最高,最高收益是多少?
24.(14分)如图,已知抛物线y=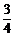 x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=
x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=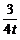 x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
(1)填空:点C的坐标是_ _,b=_ _,c=_ _;
(2)求线段QH的长(用含t的式子表示);
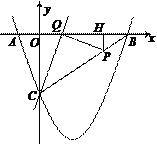 (3)依点P的变化,是否存在t的值,使以P、H、Q为顶点的三角形与△COQ相似?若存在,求出所有t的值;若不存在,说明理由.
(3)依点P的变化,是否存在t的值,使以P、H、Q为顶点的三角形与△COQ相似?若存在,求出所有t的值;若不存在,说明理由.
祝贺你顺利完成全部问题! 接下来该开始 检查了.
检查了.



