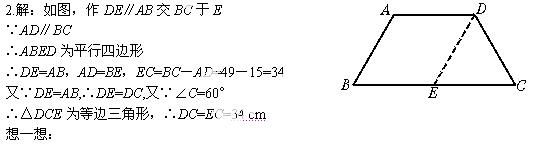1.梯形的定义是：_____________________________________________________________

_______________________________________________________________.

2.等腰梯形的定义是：_________________________________________________________

_______________________________________________________________.

3.等腰梯形的性质是：_________________________________________________________

________________________________________________.

4.在梯形中，不是同一底上的两组角的比值分别为1∶3和3∶7，则四个角的度数为.

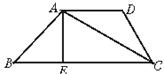
5.如图1,梯形ABCD中，AD∥BC，AC为对角线，AE⊥BC于E，AB⊥AC，若∠ACB=30°，BE=2.则BC=___________.　　　　　　　　 图1

6.直角梯形的定义是：_________________________________________________________

___________________________________________________________________________________________________________________________.

7.直角梯形一腰长16 cm,和一个底所成的角为30°,那么另一腰长________ cm.

8.等腰梯形的两底差等于腰长，腰与下底边的夹角为________，与上底的夹角为________.

9.满足条件的梯形是等腰梯形.

10.等腰梯形有下列性质：

①从角看：在同一底上的两个角________________________________________________；

②从边看：两腰_____________________________________________________________；

③从对角线看：两条对角线___________________________________________________；

④从图形的对称性看：是________对称图形.

　　　　　　

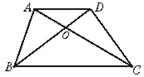
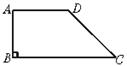
图2　　　　　　　　　　　　　　　　 图3

2.如图3，在直角梯形ABCD中，AB=4 cm,AD=4.5 cm,∠C=30°,则DC= cm，BC= cm(　　 )

A.8,4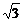　　　　　　　　　　　　　　　　　　 B.8 cm,(4.5+4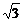) cm

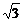C.4(+1)+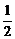,8　　　　　　　　 　　　　 D.8 cm,(4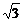+4) cm

3.等腰直角三角形各边中点连线围成的多边形是(　　 )

A.平行四边形　　　　　　　　　　　　　　　　 B.等腰三角形

C.等腰直角三角形　　　　　　　　　　　　　　 D.等边三角形

1.用下面的方法来证明：在同一底上的两个角相等的梯形是等腰梯形.

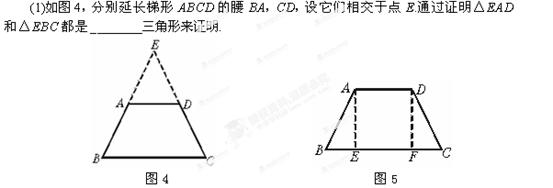(2)如图5，作梯形ABCD的高AE，DF，通过证明Rt△ABE≌Rt△DCF来证明定理.

证明过程：

(1)______________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

___________________________________________________________________________

(2)______________________________________________________________________

___________________________________________________________________________

__________________________________________________________________________

___________________________________________________________________________

2.已知等腰梯形的锐角等于60°，它的两底分别为15 cm,49 cm,求它的腰长.

在研究等腰梯形时，常常通过辅助线，使等腰梯形与等腰三角形联系起来.

想一想，用怎样的辅助线可以在等腰梯形中划出等腰三角形.

测验评价结果：_____________；对自己想说的一句话是：______________________.