
1.(3分)﹣4的绝对值是( )
|
|
A. |
 |
B. |
 |
C. |
4 |
D. |
﹣4 |
2.(3分)下列各式计算正确的是( )
|
|
A. |
(a+b)2=a2+b2 |
B. |
a2+a3=a5 |
C. |
a8÷a2=a4 |
D. |
a•a2=a3 |
3.(3分)如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是( )

|
|
A. |
40° |
B. |
50° |
C. |
60° |
D. |
140° |
4.(3分)已知一组数据:12,5,9,5,14,下列说法不正确的是( )
|
|
A. |
平均数是9 |
B. |
中位数是9 |
C. |
众数是5 |
D. |
极差是5 |
5.(3分)如图,已知AB、CD是⊙O的两条直径,∠ABC=28°,那么∠BAD=( )

|
|
A. |
28° |
B. |
42° |
C. |
56° |
D. |
84° |
6.(3分)如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )

|
|
A. |
美 |
B. |
丽 |
C. |
云 |
D. |
南 |
7.(3分)如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )

|
|
A. |
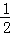 |
B. |
 |
C. |
 |
D. |
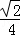 |
8.(3分)已知点P(2a﹣1,1﹣a)在第一象限,则a的取值范围在数轴上表示正确的是( )
|
|
A. |
 |
B. |
 |
C. |
 |
D. |
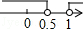 |
9.(3分)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )

|
|
A. |
a>0 |
B. |
3是方程ax2+bx+c=0的一个根 |
|
|
C. |
a+b+c=0 |
D. |
当x<1时,y随x的增大而减小 |
10.(3分)如图所示是某公园为迎接“中国﹣﹣南亚博览会”设置的一休闲区.∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )

|
|
A. |
(10π )米2 )米2 |
B. |
(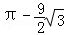 )米2 )米2 |
C. |
(6π )米2 )米2 |
D. |
(6 )米2 )米2 |
11.(3分)根据云南省统计局发布我省生产总值的主要数据显示:去年生产总值突破万亿大关,2013年第一季度生产总值为226 040 000 000元人民币,增速居全国第一.这个数据用科学记数法可表示为 2.2604×1011 元.
12.(3分)实数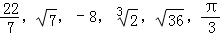 中的无理数是
中的无理数是 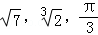 .
.
13.(3分)因式分解:2x2﹣18= 2(x+3)(x﹣3) .
14.(3分)如图,AF=DC,BC∥EF,只需补充一个条件 BC=EF ,就得△ABC≌△DEF.

15.(3分)使代数式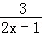 有意义的x的取值范围是 x≠
有意义的x的取值范围是 x≠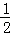 .
.
16.(3分)如图,AB是⊙O的直径,弦BC=4cm,F是弦BC的中点,∠ABC=60°.若动点E以1cm/s的速度从A点出发在AB上沿着A→B→A运动,设运动时间为t(s)(0≤t<16),连接EF,当△BEF是直角三角形时,t(s)的值为 4s .(填出一个正确的即可)
17.(3分) 如图中每一个小方格的面积为1,则可根据面积计算得到如下算式:1+3+5+7+…+(2n﹣1)= n2 (用n表示,n是正整数)

18.(6分)计算: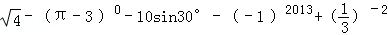 .
.
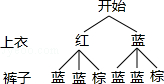
19.(5分)小明有2件上衣,分别为红色和蓝色,有3条裤子,其中2条为蓝色、1条为棕色.小明任意拿出1件上衣和1条裤子穿上.请用画树状图或列表的方法列出所有可能出现的结果,并求小明穿的上衣和裤子恰好都是蓝色的概率.
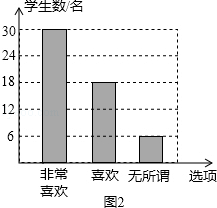
20.(5分)为了推动课堂教学改革,打造高效课堂,配合地区“两型课堂”的课题研究,羊街中学对八年级部分学生就一学期以来“分组合作学习”方式的支持程度进行调查,统计情况如图1.请根据图中提供的信息,回答下列问题.
(1)求本次被调查的八年级学生的人数,并补全条形统计图2;
(2)若该校八年级学生共有540人,请你计算该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?

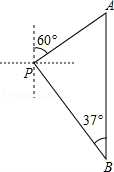
21.(5分)小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ≈1.41,
≈1.41, ≈1.73)
≈1.73)
22.(6分)如图,直线y=k1x+b(k1≠0)与双曲线y=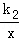 (k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.
(k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.
(1)求直线和双曲线的解析式.
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系式.
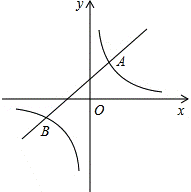
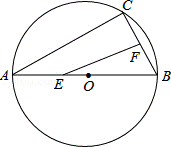
23.(7分)如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠B=60°.
(1)求∠ADC的度数;
(2)求证:AE是⊙O的切线.

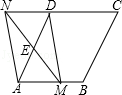
24.(7分)如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长 ME交CD的延长线于点N,连接MD,AN.
ME交CD的延长线于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形.
(2)当AM的值为何值时,四边形AMDN是矩形?请说明理由.
25.(8分)如图1,已知A(3,0)、B(4,4)、原点O(0,0)在抛物线y=ax2+bx+c (a≠0)上.
(1)求抛物线的解析式.
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只 有一个交点D,求m的值及点D的坐标.
有一个交点D,求m的值及点D的坐标.
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P的坐标(点P、O、D分别与点N、O、B对应)

26.(12分)已知一个口袋中装有7个只有颜色不同、其它都相同的球,其中3个白球、4个黑球.
(1)求从中随机取出一个黑球的概率.
(2)若往口袋中再放入x个黑球,且从口袋中随机取出一个白球的概率是 ,求代数式
,求代数式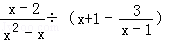 的值.
的值.
27.(12分)为提醒人们节约用水,及时修好漏水的水龙头.两名同学分别做了水龙头漏水实验,他们用于接水的量筒最大容量为100毫升.
实验一:小王同学在做水龙头漏水实验时,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升):
|
时间t(秒) |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
|
漏出的水量V(毫升) |
2 |
5 |
8 |
11 |
14 |
17 |
20 |
(1)在图1的坐标系中描出上表中数据对应的点;

(2)如果小王同学继续实验,请探求多少秒后量筒中的水会满而溢出(精确到1秒)?
(3)按此漏水速度,一小时会漏水 1.1 千克(精确到0.1千克)
实验二:
小李同学根据自己的实验数据画出的图象如图2所示,为什么图象中会出现与横轴“平行” 的部分?
的部分?
28.(12分)如图,在⊙C的内接△AOB中,AB=AO=4,tan∠AOB=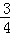 ,抛物线y=a(x﹣2)2+m(a≠0)经过点A(4,0)与点(﹣2,6).
,抛物线y=a(x﹣2)2+m(a≠0)经过点A(4,0)与点(﹣2,6).
(1)求抛物线的解析式;
(2)直线m与⊙C相切于点A,交y轴于点D,动点P在线段OB上,从点O出发向点B运动,同时动点Q在线段DA上,从点D出发向点A运动,点P的速度为每秒1个单位长,点Q的速度为每秒2个单位长.当PQ⊥AD时,求运动时间t的值.

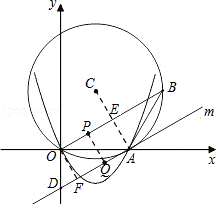
29.(14分)已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.
(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.

1.C
2.D
3.A
4.D
5.A
6.D
7.B
8.C
9.B
10.C
11. 2.2604×1011 .
12. 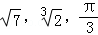 .
.
13. 2(x+3)(x﹣3) .
14. BC=EF .
15. x≠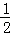 .
.
16. 4s .
17. n2
18.解:原式=2﹣1﹣5+1+9,
=6.
19.解:画树状图得:
如图:共有6种可能出现的结果,
∵小明穿的上衣和裤子恰好都是蓝色的有2种情况,
∴小明穿的上衣和裤子恰好都是蓝色的概率为: =
= .
.
20.解:(1)∵喜欢“分组合作学习”方式的圆心角度数为120°,频数为18,
∴喜欢“分组合作学习”方式的总人数为:18÷ =54人,
=54人,
故非常喜欢“分组合作学习”方式的人数为:54﹣18﹣6=30人,如图所示补全条形图即可;
(2)∵“非常喜欢”和“喜欢”两种情况在扇形统计图中所占圆心角为:120°+200°=320°,
∴支持“分组合作学习”方式所占百分比为: ×100%,
×100%,
∴该校八年级学生共有540人,有540× =480名学生支持“分组合作学习”方式.
=480名学生支持“分组合作学习”方式.
21.解:过P作PC⊥AB于C,
在Rt△APC中,AP=200m,∠ACP=90°,∠PAC=60°.
∴PC=200×sin60°=200× =100
=100 .
.
∵在Rt△PBC中,sin37°= ,
,
∴PB= =
= ≈288(m),
≈288(m),
答:小亮与妈妈相距约288米.

22.解:(1)∵双曲线y=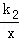 经过点B(﹣2,﹣1),
经过点B(﹣2,﹣1),
∴k2=2,
∴双曲线的解析式为:y= ,
,
∵点A(1,m)在双曲线y= 上,
上,
∴m=2,即A(1,2),
由点A(1,2),B(﹣2,﹣1)在直线y=k1x+b上,得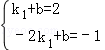 ,
,
解得: ,
,
∴直线的解析式为:y=x+1;
(2)∵A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,
∴A1与A2在第三象限,A3在第一象限,即y1<0,y2<0,y3>0,
则y2<y1<y3.
23.解:(1)∵∠ABC与∠ADC都是弧AC所对的圆周角,
∴∠ADC=∠B=60°.
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=30°.
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,即 BA⊥AE.
∴AE是⊙O的切线.
24. (1)证明:∵四边形ABCD是菱形,
∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME,
∵点E是AD中点,
∴DE=AE,
在△NDE和△MAE中,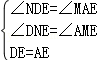 ,
,
∴△NDE≌△MAE(AAS),
∴ND=MA,
∴四边形AMDN是平行四边形;
(2)AM=1.
理由如下:∵四边形ABCD是菱形,
∴AD=AB=2,
∵平行四边形AMDN是矩形,
∴DM⊥AB,
即∠DMA=90°,
∵∠A=60°,
∴∠ADM=30°,
∴AM= AD=1.
AD=1.
25.解:(1)∵A(3,0)、B(4,4)、O(0,0)在抛物线y=ax2+bx+c (a≠0)上.
∴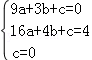 ,
,
解得: ,
,
故抛物线的解析式为:y=x2﹣3x;
(2)设直线OB的解析式为y=k1x( k1≠0),
由点B(4,4)得
4=4 k1,
解得k1=1.
∴直线OB的解析式为y=x,∠AOB=45°.
∵B(4,4),
∴点B向下平移m个单位长度的点B′的坐标为(4,0),
故m=4.
∴平移m个单位长度的直线为y=x﹣4.
解方程组 
解得: ,
,
∴点D的坐标为(2,﹣2).
(3)∵直线OB的解析式y=x,且A(3,0).
∵点A关于直线OB的对称点A′的坐标为(0,3).
设直线A′B的解析式为y=k2x+3,此直线过点B(4,4).
∴4k2+3=4,
解得 k2=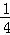 .
.
∴直线A′B的解析式为y=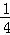 x+3.
x+3.
∵∠NBO=∠ABO,∴点N在直线A′B上,
设点N(n,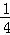 n+3),又点N在抛物线y=x2﹣3x上,
n+3),又点N在抛物线y=x2﹣3x上,
∴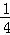 n+3=n2﹣3n.
n+3=n2﹣3n.
解得
n1= ,n2=4(不合题意,舍去),
,n2=4(不合题意,舍去),
∴点N的坐标为(﹣ ,
, ).
).
如图,将△NOB沿x轴翻折,得到△N1OB1,
则 N1 (﹣ ,﹣
,﹣ ),B1(4,﹣4).
),B1(4,﹣4).
∴O、D、B1都在直线y=﹣x上.
∵△P1OD∽△NOB,
∴△P1OD∽△N1OB1,
∴P1为O N1的中点.
∴ =
= =
= ,
,
∴点P1的坐标为(﹣ ,﹣
,﹣ ).
).
将△P1OD沿直线y=﹣x翻折,可得另一个满足条件的点到x轴距离等于P1到y轴距离,点到y轴距离等于P1到x轴距离,
∴此点坐标为:( ,
, ).
).
综上所述,点P的坐标为(﹣ ,﹣
,﹣ )和(
)和( ,
, ).
).

26.解:(1)P(取出一个黑球)= =
= .
.
(2)设往口袋中再放入x个黑球,从口袋中随机取出一个白球的概率是 ,
,
即
P(取出一个白球)=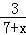 =
= .
.
由此解得x=5.
经检验x=5是原方程的解.
∵原式= ÷
÷
= ×
×
= ,
,
∴当x=5时,原式=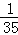 .
.
27.解:实验一:
(1)画图象如图所示:

(2)设V与t的函数关系式为V=kt+b,
根据表中数据知:
当t=10时,V=2;
当t=20时,V=5,
所以 ,
,
解得: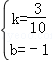 ,
,
所以V与t的函数关系式为V=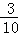 t﹣1,
t﹣1,
由题意得: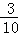 t﹣1≥100,
t﹣1≥100,
解得t≥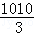 =336
=336 ,
,
所以337秒后,量筒中的水会满面开始溢出;
(3)一小时会漏水 ×3600﹣1=1079(毫升)=1079(克)≈1.1千克;
×3600﹣1=1079(毫升)=1079(克)≈1.1千克;
故答案为:1.1;
实验二:
因为小李同学接水的量筒装满后开始溢出,量筒内的水位不再发生变化,
所以图象中会出现与横轴“平行”的部分.
28.解:(1)将点A(4,0)和点(﹣2,6)的坐标代入y=a(x﹣2)2+m中,得方程组,

解得 ,
,
故抛物线的解析式为y= x2﹣2x.
x2﹣2x.
(2)如图所示,连接AC交OB于E.作OF⊥AD于F,
∵直线m切⊙C于点A,
∴AC⊥m.
∵弦AB=AO,
∴ =
= .
.
∴AC⊥OB,
∴m∥OB.
∴∠OAD=∠AOB.
∵OA=4,tan∠AOB=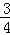 ,
,
∴OD=OA•tan∠OAD=4×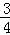 =3.
=3.
则OF=OA•sin∠OAD=4× =2.4.
=2.4.
t秒时,OP=t,DQ=2t,
若PQ⊥AD,则 FQ=OP=t.DF=DQ﹣FQ=t.
∴△ODF中,t=DF=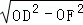 =1.8(秒).
=1.8(秒).
29.(1)证明:∵菱形AFED,
∴AF=AD,
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°=∠DAF,
∴∠BAC﹣∠DAC=∠DAF﹣∠DAC,
即∠BAD=∠CAF,
∵在△BAD和△CAF中
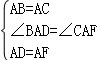 ,
,
∴△BA D≌△CAF,
D≌△CAF,
∴CF=BD,
∴CF+CD=BD+CD=BC=AC,
即①BD=CF,②AC=CF+CD.
(2)解:AC=CF+CD不成立,AC、CF、CD之间存在的数量关系是AC=CF﹣CD,
理由是:由(1)知:AB=AC=BC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC+∠DAC=∠DAF+∠DAC,
即∠BAD=∠CAF,
∵在△BAD和△CAF中
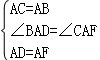 ,
,
∴△BAD≌△CAF,
∴BD=CF,
∴CF﹣CD=BD﹣CD=BC=AC,
即AC=CF﹣CD.
(3)AC=CD﹣CF.理由是:
∵∠BAC=∠DAF=60 °,
°,
∴∠DAB=∠CAF,
∵在△BAD和△CAF中
 ,
,
∴△BAD≌△CAF,
∴CF=BD,
∴CD﹣CF=CD﹣BD=BC=AC,
即AC=CD﹣CF.
