1.在下列“回收”、“和平”、“志愿者”、“节水”这四个标志中,属于轴对称图形的是( )
A. B.
B.  C..
C..  D.
D. 
2.在平面直角坐标系中,点P(2,-3)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列各组数据,能作为直角三角形三边长的是 ( )
A.11,15,13 B.1,4,5 C.8,15,17 D.4,5,6
4.如果等腰三角形两边长是6cm和3cm,那么它的周长是 ( )
A.9cm B.12cm C.15cm或12cm D.15cm
5.一次函数 的图象不经过的象限是
( )
的图象不经过的象限是
( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.数3.949×105精确到万位,用科学计数法可以表示为 ( )
A.39×104 B.3.9×105 C.3.95×105 D.4.0×105
7.如果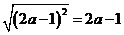 ,那么
,那么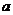 的取值范围
(
)
的取值范围
(
)
A. B.
B. C.
C. D.
D.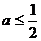
8.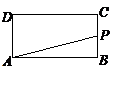
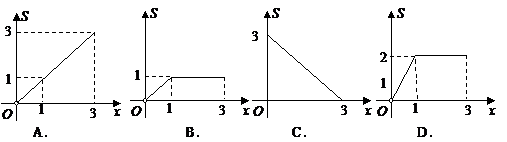 如图,在矩形
如图,在矩形 中,AB=2,
中,AB=2,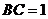 ,动点P从点B出发,沿路线
,动点P从点B出发,沿路线 作匀速运动,那么能反应
作匀速运动,那么能反应 的面积S与点P运动的路程
的面积S与点P运动的路程 之间的函数图像是
( )
之间的函数图像是
( )
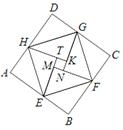
9.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=15,则S2的值是 ( )
A. 3 B. C. 5 D.
10.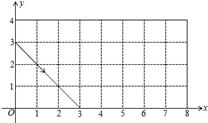 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P的坐标为(
)
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P的坐标为(
)
A.(1,4) B.(5,0) C.(6,4) D.(8,3)
11. 计算
计算 = ;27的平方根是
。
= ;27的平方根是
。
12. 函数 中,自变量
中,自变量 的取值范围是 ;实数2-
的取值范围是 ;实数2- 的倒数是
。
的倒数是
。
13.一个直角三角形,两直角边长分别为5和12,则斜边长为 .
14.点M(3,-4)关于y轴的对称点N的坐标是_________ 。
15. 将直线y=2x﹣1向上平移5个单位长度后再向左平移3个单位后所得的直线解析式是
.
将直线y=2x﹣1向上平移5个单位长度后再向左平移3个单位后所得的直线解析式是
.
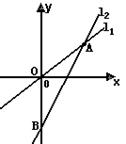
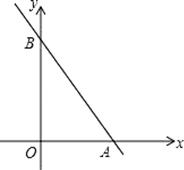
16.如图:已知两直线l1和l2相交于点A(4,3),且OA=OB,则点B的坐标为 .
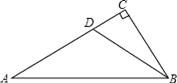
17.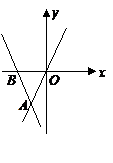 如图,在Rt△ABC中,∠C=90°,D为AC上的一点,且DA=DB=5,又△DAB的面积为10,那么DC的长是
.
如图,在Rt△ABC中,∠C=90°,D为AC上的一点,且DA=DB=5,又△DAB的面积为10,那么DC的长是
.
18.如图,直线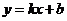 经过点
经过点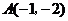 和点
和点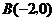 ,
,
不等式 的解集为
.
的解集为
.
19.(本题8分)
(1)计算: (2)
(2)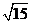 ×
×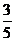
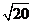 ÷(-
÷(-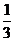
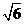 )
)
20.(本题6分)解方程:①8 x3+125=0 ②5(x+1)2-100=0
21.(本题5分)如图,在平面直角坐标系xOy中,点A(0,8),点B(10,2).
(1)只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件(要求保留作图痕迹,不必写出作法):
①点P到A、B两点的距离相等;②点P到∠xOy的两边距离相等.
(2)若在x轴上有点M,则能使△ABM的周长最小的点M的坐标为 .

|

22.(本题5分)已知如图所示,四边形ABCD中,AB=6cm,AD=8cm,BC=26cm,CD=24cm ,求四边形ABCD的面积.
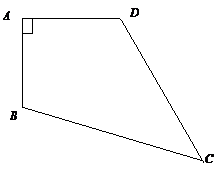

23.(本题5分)如图在△ABC和△DAE中,∠DAE=∠BAC,AB=AE,AD=AC,连接BD、CE.
求证:BD=CE

24. (本题5分)在直角坐标系xOy中,直线l过(1,3)和(2,1)两点,且与x轴,y轴分别交于A,B两点.
 (1)求直线l的函数关系式;(2)求△AOB的面积.
(1)求直线l的函数关系式;(2)求△AOB的面积.

25.(本题8分)已知:如图1,射线MN⊥AB,AM=1cm,MB=4cm. 点C从M出发以2cm/s的 速度沿射线MN运动,设点 C的运动时间为t(s)。
(1)当△ABC为等腰三角形时,求t的值;(2)当△ABC为直角三角形时,求t的值;
(3)当t满足条件:__________时,△ABC为钝角三角形; 当_________时,△ABC为锐角三角形.

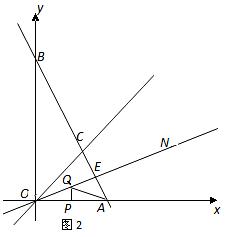
26.(本题8分)如图1,在平面直角坐标系中,直线AB与 轴交于点A,与
轴交于点A,与 轴交于点B,与直线OC交于点C.
轴交于点B,与直线OC交于点C.
(1) 若直线AB解析式为 ,直线OC的解析式是y=x,
,直线OC的解析式是y=x,
①求点C的坐标;②求△OAC的面积.

(2) 如图2,作 的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.
的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.