
1、已知二次函数的图像开口向下,且与y轴的正半轴相交,请你写出一个满足上述条件的二次函数的解
析式:
2、已知x为实数,且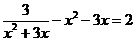 ,那么
,那么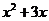 的值为
的值为
3、2003年信息产业部的统计数据表明,截止到10月底,我国的电话用户总数达到5.12亿,居世界首位。
其中5.12亿用科学记数法表示为 。
4、某种商品的进价为m元,在销售旺季,该商品售价较进价高50%;销售旺季过后,又以7折的价格对该商品开展促销活动,这时一件该商品的售价为 (用含m的代数式表示)
5、已知反比例函数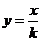 (k≠0),当x<0时,y随x的增大而增大,那么一次函数y=kx-k的图像不
(k≠0),当x<0时,y随x的增大而增大,那么一次函数y=kx-k的图像不
经过 象限。
6、如图1,E、F、G、H分别是正方形ABCD各边的中点,要使中间阴影部分小正方形的面积为5,则大
正方形的边长应该为
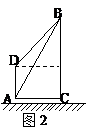
7、如图2,有甲、乙两楼,甲楼高AD为23米,某人在甲楼的楼底A和楼顶D,分别测得乙楼的楼顶B
的仰角为65º13’和45º,利用这些数据可求乙楼高度为 米(精确到0.01米,tan65º13’=2.166)
8、在① 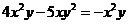 ;②
;②
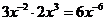 ;③
;③ 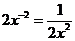 ;④
;④ 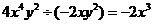
上述运算中正确的是 。
9、一幅美丽的图像,在某个顶点处由四个边长相等的正多边形镶嵌而成,其中的三个分别为正三角形、
正四边形、正六边形,那么另外一个为 。
10、甲乙两个工程队完成某项工程,首先是甲单独完成了10天,然后乙队加入合作,完成剩下的全部工
程,设工程总量为单位1,工程进度满足如图3所示的函数关系,那么实际完成这项工程所用的时间
比由甲单独完成这项工程所需时间少 天。
11、下列等式中:① 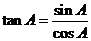 ;②
;②
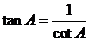 ;③
;③ 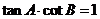 ;④
;④ 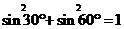
不成立的是 。
12、如图4所示电路的总电阻为10Ω,若R1=2R2,则R1和R2的值分别是 。
13、如图5,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N,P、Q分别是弧AM、弧BM上
一点(不与端点重合),如果∠MNP=∠MNQ,给出下列结论:① ∠1=∠2;② ∠P+∠Q=180º;
③ ∠Q=∠PMN;④ PM=QM;⑤ MN2=PN•QN,则其中正确的序号是 。
14、如图6⑴,在正方形铁皮上剪下一个圆形和扇形,使之恰好围成如图6⑵所示的一个圆锥模型,设圆


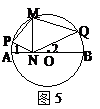
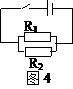
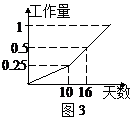
 的半径为r,扇形半径为R,则圆的半径与扇形半径之间的关系为
。
的半径为r,扇形半径为R,则圆的半径与扇形半径之间的关系为
。
15、如图7,在方格纸中,每个小方格都是边长为1的正方形。点A、B是方格纸中的两个格点(即正方形
的顶点),在这个5×5的方格纸中,请你找出格点C,使△ABC的面积为2个平方单位,则满足条件
的格点C的个数有 个。
16、某商场六月份随机抽查了6天的营业额,结果分别如下(单位:万元):2.8,3.2,3.4,3.4,3.0,
3.4问:这6天的营业额的众数是 万元,估计该商场六月份的总营业额约是
万元
17、先化简,再求值
 ,其中
,其中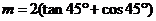

18、右图是一只蝴蝶图案的一部分,请你利用尺规作图:把图(实线部分)
 补成以虚线l为对称轴的轴对称图形,这时,你会得到一只美丽蝴蝶
补成以虚线l为对称轴的轴对称图形,这时,你会得到一只美丽蝴蝶
的完整图案(不写作法,保留作图痕迹)
19、甲、乙两人在相同的条件下各射靶10次,射靶的成绩如图所示:
⑴ 请根据图中信息完成下表
|
项目 |
平均数 |
中位数 |
方差 |
6.5-7.5环的频数 |
6.5-7.5环的频率 |
|
甲 |
7 |
7.5 |
4.2 |
2 |
 0.2 0.2 |
|
乙 |
|
|
|
|
|
⑵ 甲乙两人谁射靶的成绩比较稳定?请说明理由
20、已知一元二次方程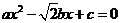 的两个根满足
的两个根满足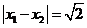 ,且a、b、c分别是△ABC的∠A、∠B、∠C的对边,若a=c,求∠B的度数
,且a、b、c分别是△ABC的∠A、∠B、∠C的对边,若a=c,求∠B的度数
小亮同学解得此题得正确答案“∠B=120º”后,思考以下问题,请你帮助解答
⑴
若在原题中,将方程改为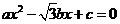 ,要得到∠B=120º,而条件“a=c”不变,那么对应条件中的
,要得到∠B=120º,而条件“a=c”不变,那么对应条件中的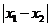 的值做怎样的改变?并说明理由;
的值做怎样的改变?并说明理由;
⑵
若在原题中,将方程改为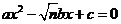 (n为正整数,n≥2),要得到∠B=120º,而条件“a=c”不变,那么条件中的
(n为正整数,n≥2),要得到∠B=120º,而条件“a=c”不变,那么条件中的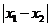 的值应改为多少?(直接写出结果,不必说明理由)
的值应改为多少?(直接写出结果,不必说明理由)
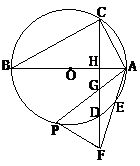
21、如图,AB为⊙O的直径,弦CD⊥AB,垂足为H
⑴ 求证: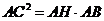
⑵ 当点B移动到点E的位置时,设弦AE的延长线与弦CD的延长线
交于点F,此时是否仍有上面的结论成立(即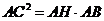 )?
)?
请说明理由
22、据电力部门统计,每天8:00至21:00是用电高峰,简称“峰时”,21:00至次日8:00是用电低谷期,简称“谷时”。为了缓解供电需求紧张的矛盾,某市电力部门拟逐步统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策。具体见下表:
|
时间 |
换表前 |
换表后 |
|
|
峰时(8:00-21:00) |
谷时(21:00-次日8:00) |
||
|
电价 |
0.52元/千瓦•时 |
x元/千瓦•时 |
y元/千瓦•时 |
已知每千瓦•时峰时价比谷时价高0.25元,小明家对换表后最初使用的100千瓦•时用电情况进行统计分析知:峰时用电量占80%,谷时用电量占20%,与换表前相比,电费共下降2元。
⑴ 请你求出表格中x和y的值;
⑵ 小明希望通过调整用电时间,使他家以后每使用100千瓦•时的电费与换表前相比下降10元至15元(包括10元和15元)。假设小明家今后“峰时”用电量占整个家庭用电量的z%,那么z在什么范围内时,才能达到小明的期望?
23、 如图,△OAB是边长为
如图,△OAB是边长为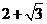 的等边三角形,其中O是坐标原点,顶点B在y轴的正方向上,将△OAB折叠,使点A落在边OB上,记为A’,折痕为EF
的等边三角形,其中O是坐标原点,顶点B在y轴的正方向上,将△OAB折叠,使点A落在边OB上,记为A’,折痕为EF
⑴ 当A’F//x轴时,求点A’和E的坐标;
⑵
当A’F//x轴时,且抛物线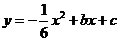 经过点A’和E时,
经过点A’和E时,
求该抛物线与x轴的交点的坐标;
⑶ 当点A’在OB上运动但不与点O、B重合时,能否使△A’EF
成为 直角三角形?若能,请求出此时A’的坐标;若不能,
请你说明理由