1．(2015.南通)如图，在平面直角坐标系中，直线OA过点(2，1)，则tanα的值是( C )
A. B. C. D．2
,第1题图) 
,第2题图) 
,第3题图)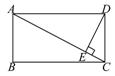 
,第4题图)
2．河堤横断面如图所示，堤高BC＝5米，迎水坡AB的坡比为1∶(坡比是坡面的铅直高度BC与水平宽度AC之比)，则AC的长是( A )
A．5米 B．10米 C．15米 D．10米
3．如图，正方形ABCD中，对角线AC，BD交于点O，点M，N分别为OB，OC的中点，则cos∠OMN的值为( B )
A. B. C. D．1
4．如图，在矩形ABCD中，DE⊥AC于E，设∠ADE＝α，且cosα＝，AB＝4，则AC的长为( C )
A．3 B. C. D.
5．如图，在四边形ABCD中，∠A＝60°，∠B＝∠D＝90°，BC＝2，CD＝3，则AB＝( D )
A．4 B．5 C．2 D.
,第5题图) 
,第6题图) 
,第9题图)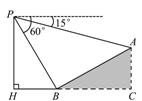 
,第10题图)
6．如图，cosB＝，sinC＝，AC＝5，则△ABC的面积是( A )
A. B．12 C．14 D．21
7．式子2cos30°－tan45°－的值是( B )
A．2－2 B．0 C．2 D．2
8．李红同学遇到了这样一道题：tan(α+20°)＝1，你认为锐角α的度数应是( D )
A．40° B．30° C．20° D．10°
9．为了测量被池塘隔开的A，B两点之间的距离，根据实际情况，作出如图图形，其中AB⊥BE，EF⊥BE，AF交BE于D，C在BD上．有四位同学分别测量出以下四组数据：①BC，∠ACB；②CD，∠ACB，∠ADB；③EF，DE，BD；④DE，DC，BC.能根据所测数据，求出A，B间距离的有( C )
A．1组 B．2组 C．3组 D．4组
10．如图，某人在大楼30米高(即PH＝30米)的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处的俯角为60°，已知该山坡的坡角i为1∶，点P，H，B，C，A在同一个平面上，点H，B，C在同一条直线上，且PH⊥HC.则A，B两点间的距离是( B )
A．15米 B．20米 C．20米 D．10米
11．若α为锐角，cosα＝，则sinα＝____，tanα＝____．
12．在Rt△ABC中，∠C＝90°，tanA＝，△ABC的周长为18，则S△ABC＝____．
13．(2015.南昌)小志同学书桌上有一个电子相框，将其侧面抽象如图所示的几何图，已知AB＝AC＝15 cm，∠BAC＝40°，则点A到BC的距离为__14.1__cm.(参考数据：sin20°≈0.342，cos20°≈0.940，sin40°≈0.643，cos40°≈0.766.结果精确到0.1 cm，可用科学计算器)
,第13题图) 
,第15题图)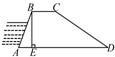 
,第16题图) 
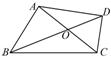,第17题图)
14．在△ABC中，若|2cosA－1|+(－tanB)2＝0，则∠C＝__60°__．
15．如图，在顶角为30°的等腰三角形ABC中，AB＝AC，若过点C作CD⊥AB于点D，则∠BCD＝15°，根据图形计算tan15°＝__2－__．
16．如图所示，某河堤的横断面是梯形ABCD，BC∥AD，迎水坡AB长13米，且tan∠BAE＝，则河堤的高BE为__12__米．
17．如图，四边形ABCD的对角线AC，BD相交于点O，且BD平分AC.若BD＝8，AC＝6，∠BOC＝120°，则四边形ABCD的面积为__12__．(结果保留根号)
18．如图，在Rt△ABC中，∠C＝90°，AC＝3，tanA＝.点D，E分别是边BC，AC上的点，且∠EDC＝∠A.将△ABC沿DE所在直线对折，若点C恰好落在边AB上，则DE的长为____．
19．(10分)解下列各题：
(1)先化简，再求代数式(+)÷的值，其中x＝cos30°+；
解：原式＝x+1，当x＝2时，原式＝3
(2)已知α是锐角，且sin(α+15°)＝.计算－4cosα－(π－3.14)0+tanα+()－1的值．
解：α＝45°，原式＝3
20．(8分)解下列各题：
(1)已知∠A，∠B，∠C是锐角三角形ABC的三个内角，且满足(2sinA－)2+＝0，求∠C的度数；
解：75°
(2)(原创题)已知tanα的值是方程x2－x－2＝0的一个根，求式子的值．
解：∵方程的根为x1＝2，x2＝－1.又∵tanα＞0，∴tanα＝2，∴原式＝＝＝
21．(10分)如图，在△ABC中，AD是BC上的高，tanB＝cos∠DAC.
(1)求证：AC＝BD；
(2)若sinC＝，BC＝12，求AD的长．
解：(1)∵AD是BC上的高，∴AD⊥BC，∴∠ADB＝90°，∠ADC＝90°，在Rt△ABD和Rt△ADC中，∵tanB＝，cos∠DAC＝，又tanB＝cos∠DAC，∴＝，∴AC＝BD (2)在Rt△ADC中，sinC＝，故可设AD＝12k，AC＝13k，∴CD＝＝5k.∵BC＝BD+CD，AC＝BD，∴BC＝13k+5k＝18k，∴18k＝12，∴k＝，∴AD＝12k＝12×＝8
22．(8分)(2015.河南)如图，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°.若坡角∠FAE＝30°，求大树的高度．(结果保留整数．参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，≈1.73)
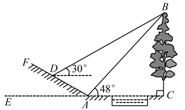
解：延长BD交AE于点G，过点D作DH⊥AE于点H.由题意知∠DAE＝∠BGA＝30°，DA＝6，∴GD＝DA＝6，∴GH＝AH＝DA.cos30°＝3，∴GA＝6.设BC的长为x米．在Rt△GBC中，GC＝＝＝x.在Rt△ABC中，AC＝＝∵GC－AC＝GA，∴x－＝6，∴x≈13，即大树的高度约为13米
23．(8分)(2015.成都)如图，登山缆车从点A出发，途经点B后到达终点C.其中AB段与BC段的运行路程均为200 m，且AB段的运行路线与水平面的夹角为30°，BC段的运行路线与水平面的夹角为42°，求缆车从点A运行到点C的垂直上升的距离．
(参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90)
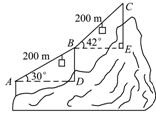
解：根据题意可知∠BAD＝30°，∠CBE＝42°，AB＝BC＝200 m．在Rt△ABD中，BD＝AB.sin30°＝200×＝100(m)．在Rt△BCE中，CE＝BC.sin42°≈200×0.67＝134(m)，∴BD+CE≈100+134＝234(m)，因此，缆车从点A运行到点C的垂直上升的距离约为234 m
24．(10分)如图是我国某海域内的一个小岛，其平面图如图甲所示，小明据此构造出该岛的一个数学模型如图乙所示，其中∠B＝∠D＝90°，AB＝BC＝15千米，CD＝3千米，请据此解答如下问题：
(1)求该岛的周长和面积；(结果保留整数，参考数据：≈1.414，≈1.732，≈2.449)
(2)求∠ACD的余弦值．
解：连结AC，∵AB＝BC＝15千米，∠B＝90°，∴∠BAC＝∠ACB＝45°，AC＝15千米，又∵∠D＝90°，∴AD＝＝＝12(千米)，∴周长＝AB+BC+CD+DA≈55(千米)，面积＝S△ABC+S△ADC≈157(平方千米)
(2)cos∠ACD＝＝＝
25．(12分)如图，甲、乙只捕捞船同时从A港出海捕鱼，甲船以每小时15 km的速度沿北偏西60°方向前进，乙船以每小时15 km的速度沿东北方向前进．甲船航行2 h到达C处，此时甲船发现渔具丢在了乙船上，于是甲船快速(匀速)沿北偏东75°的方向追赶乙船，结果两船在B处相遇．问：
(1)甲船从C处出发追赶上乙船用了多少时间？
(2)甲船追赶乙船的速度是每小时多少千米？
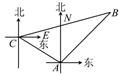
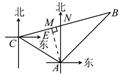
解：过点A作AM⊥BC于点M，如图，(1)设甲船从C处出发追赶上乙船用了x h，则乙船从A到B用了(x+2)h.在Rt△ACM中，AC＝15×2＝30(km)，∴MC＝AM＝AC.sin∠ACB＝30×＝30(km)．在Rt△ABM中，AM＝AB，∴30＝×15×(x+2)，解得x＝2，答：甲船从C处出发追赶上乙船用了2 h (2)在Rt△ABM中，AM＝30 km，AB＝60 km，∴BM＝＝＝30(km)，∴BC＝MC+BM＝30(1+)(km)，∴甲船追赶乙船的速度是＝15(1+)km/h.答：甲船追赶乙船的速度是每小时15(1+)千米
