
1.已知集合A={x|x<1},B={x|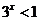 },则
},则
A. B.
B.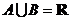
C.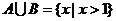 D.
D.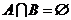
[答案]A

2.如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是

A.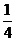 B.
B.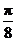
C. D.
D.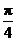
[答案]B
[解析]
试题分析:设正方形边长为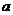 ,则圆的半径为
,则圆的半径为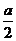 ,则正方形的面积为
,则正方形的面积为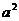 ,圆的面积为
,圆的面积为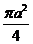 .由图形的对称性可知,太极图中黑白部分面积相等,即各占圆面积的一半.由几何概型概率的计算公式得,此点取自黑色部分的概率是
.由图形的对称性可知,太极图中黑白部分面积相等,即各占圆面积的一半.由几何概型概率的计算公式得,此点取自黑色部分的概率是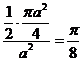 ,选B.
,选B.
秒杀解析:由题意可知,此点取自黑色部分的概率即为黑色部分面积占整个面积的比例,由图可知其概率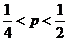 ,故选B.
,故选B.
[考点]几何概型
[名师点睛]对于几何概型的计算,首先确定事件类型为几何概型并确定其几何区域(长度、面积、体积或时间),其次计算基本事件区域的几何度量和事件A区域的几何度量,最后计算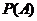 .
.
3.设有下面四个命题
 :若复数
:若复数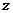 满足
满足 ,则
,则 ;
;
 :若复数
:若复数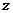 满足
满足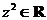 ,则
,则 ;
;
 :若复数
:若复数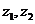 满足
满足 ,则
,则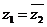 ;
;
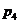 :若复数
:若复数 ,则
,则 .
.
其中的真命题为
A. B.
B.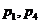 C.
C.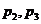 D.
D.
[答案]B

4.记 为等差数列
为等差数列 的前
的前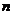 项和.若
项和.若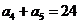 ,
, ,则
,则 的公差为
的公差为
A.1 B.2 C.4 D.8
[答案]C
[解析]
试题分析:设公差为 ,
, ,
,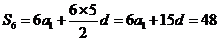 ,联立
,联立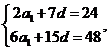 解得
解得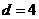 ,故选C.
,故选C.
秒杀解析:因为 ,即
,即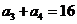 ,则
,则 ,即
,即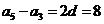 ,解得
,解得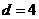 ,故选C.
,故选C.
[考点]等差数列的基本量求解
[名师点睛]求解等差数列基本量问题时,要多多使用等差数列的性质,如 为等差数列,若
为等差数列,若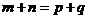 ,则
,则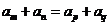 .
.
5.函数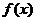 在
在 单调递减,且为奇函数.若
单调递减,且为奇函数.若 ,则满足
,则满足 的
的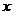 的取值范围是
的取值范围是
A. B.
B.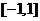 C.
C. D.
D.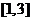
[答案]D
6.
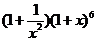 展开式中
展开式中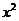 的系数为
的系数为
A.15 B.20 C.30 D.35
[答案]C
[解析]
试题分析:因为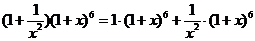 ,则
,则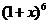 展开式中含
展开式中含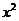 的项为
的项为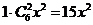 ,
,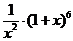 展开式中含
展开式中含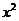 的项为
的项为 ,故
,故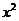 前系数为
前系数为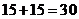 ,选C.
,选C.
[考点]二项式定理
[名师点睛]对于两个二项式乘积的问题,第一个二项式中的每项乘以第二个二项式的每项,分析好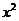 的项共有几项,进行加和.这类问题的易错点主要是未能分析清楚构成这一项的具体情况,尤其是两个二项式展开式中的
的项共有几项,进行加和.这类问题的易错点主要是未能分析清楚构成这一项的具体情况,尤其是两个二项式展开式中的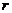 不同.
不同.
7.某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为
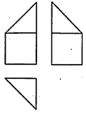
A.10 B.12 C.14 D.16
[答案]B

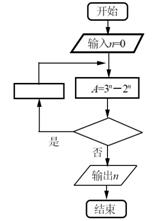
8.右面程序框图是为了求出满足3n−2n>1000的最小偶数n,那么在 和
和 两个空白框中,可以分别填入
两个空白框中,可以分别填入
A.A>1 000和n=n+1
B.A>1 000和n=n+2
C.A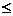 1 000和n=n+1
1 000和n=n+1
D.A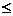 1 000和n=n+2
1 000和n=n+2
[答案]D
9. 已知曲线C1:y=cos
x,C2:y=sin (2x+
已知曲线C1:y=cos
x,C2:y=sin (2x+ ),则下面结论正确的是
),则下面结论正确的是
A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线C2
个单位长度,得到曲线C2
[答案]D
[解析]
试题分析:因为 函数名不同,所以先将
函数名不同,所以先将 利用诱导公式转化成与
利用诱导公式转化成与 相同的函数名,则
相同的函数名,则 ,则由
,则由 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的 倍变为
倍变为 ,再将曲线向左平移
,再将曲线向左平移 个单位得到
个单位得到 ,故选D.
,故选D.
[考点]三角函数图像变换.
[名师点睛]对于三角函数图像变换问题,首先要将不同名函数转换成同名函数,利用诱导公式,需要重点记住 ;另外,在进行图像变换时,提倡先平移后伸缩,而先伸缩后平移在考试中经常出现,无论哪种变换,记住每一个变换总是对变量
;另外,在进行图像变换时,提倡先平移后伸缩,而先伸缩后平移在考试中经常出现,无论哪种变换,记住每一个变换总是对变量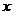 而言.
而言.
10.已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为
A.16 B.14 C.12 D.10
[答案]A

 ,所以
,所以
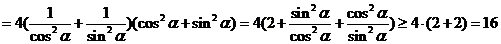
11.设x、y、z为正数,且 ,则
,则
A.2x<3y<5z B.5z<2x<3y C.3y<5z<2x D.3y<2x<5z
[答案]D

绝密启用前 2017年普通高等学校招生全国统一考试 课标1理科数学 2017年全国1高考数学与2016全国1高考数学难度方面相对持平,在选择题和填空题方面难度有所提升,解答题方面难度有所减缓.在保持稳定的基础上,进行适度创新,尤其是选择填空压轴题.试卷内容上体现新课程理念,贴近中学数学教学,坚持对基础性的考查,同时加大了综合性、应用性和创新性的考查,如理科第2、3、10、11、12、16、19题,文科第2、4、9、12、19题. 1.体现新课标理念,重视对传统核心考点考查的同时,增加了对数学文化参考答案
12.几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是
A.440 B.330 C.220 D.110
[答案]A
[解析]试题分析:由题意得,数列如下:
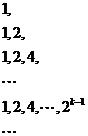
则该数列的前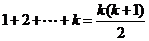 项和为
项和为
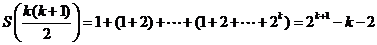
要使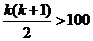 ,有
,有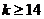 ,此时
,此时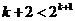 ,所以
,所以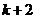 是之后的等比数列
是之后的等比数列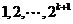 的部分和,即
的部分和,即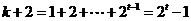 ,
,
所以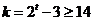 ,则
,则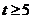 ,此时
,此时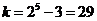 ,
,
对应满足的最小条件为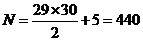 ,故选A.
,故选A.
[考点]等差数列、等比数列的求和.
[名师点睛]本题非常巧妙的将实际问题和数列融合在一起,首先需要读懂题目所表达的具体含义,以及观察所给定数列的特征,进而判断出该数列的通项和求和.另外,本题的难点在于数列里面套数列,第一个数列的和又作为下一个数列的通项,而且最后几项并不能放在一个数列中,需要进行判断.
二、填空题:本题共4小题,每小题5分,共20分.
13.已知向量a,b的夹角为60°,|a|=2,|b|=1,则| a +2 b |= .
[答案]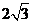

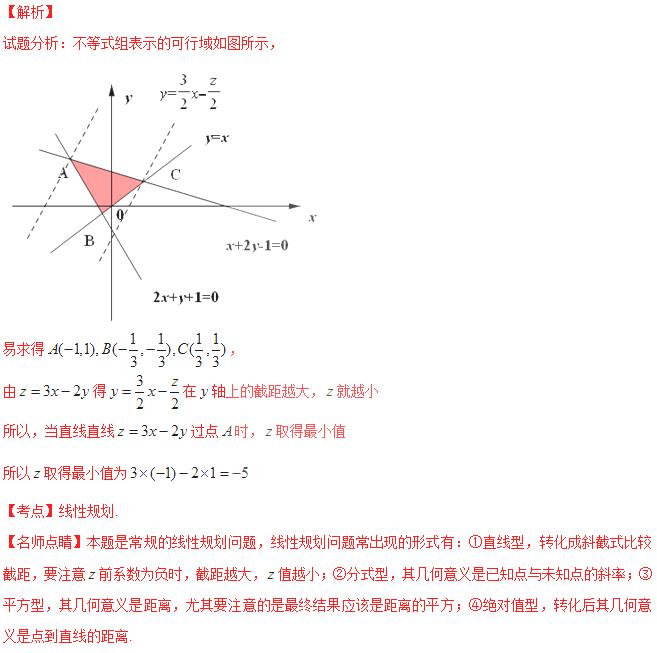
14.设x,y满足约束条件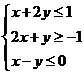 ,则
,则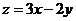 的最小值为
.
的最小值为
.
[答案]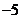
15.已知双曲线C: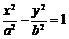 (a>0,b>0)的右顶点为A,以A为圆心,b为半径作圆A,圆A与双曲线C的一条渐近线交于M、N两点.若∠MAN=60°,则C的离心率为________.
(a>0,b>0)的右顶点为A,以A为圆心,b为半径作圆A,圆A与双曲线C的一条渐近线交于M、N两点.若∠MAN=60°,则C的离心率为________.
[答案]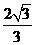
 [考点]双曲线的简单性质.
[考点]双曲线的简单性质.
[名师点睛]双曲线渐近线是其独有的性质,所以有关渐近线问题受到出题者的青睐.做好这一类问题要抓住以下重点:①求解渐近线,直接把双曲线后面的1换成0即可;②双曲线的焦点到渐近线的距离是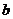 ;③双曲线的顶点到渐近线的距离是
;③双曲线的顶点到渐近线的距离是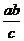 .
.
16.如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______.
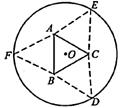
[答案]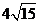

[考点]简单几何体的体积
[名师点睛]对于三棱锥最值问题,肯定需要用到函数的思想进行解决,本题解决的关键是设好未知量,利用图形特征表示出三棱锥体积.当体积中的变量最高次是2次时可以利用二次函数的性质进行解决,当变量是高次时需要用到求导得方式进行解决.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)
△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为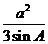
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
 [考点]三角函数及其变换.
[考点]三角函数及其变换.
[名师点睛]在处理解三角形问题时,要注意抓住题目所给的条件,当题设中给定三角形的面积,可以使用面积公式建立等式,再将所有边的关系转化为角的关系,有时需将角的关系转化为边的关系;解三角形问题常见的一种考题是“已知一条边的长度和它所对的角,求面积或周长的取值范围”或者“已知一条边的长度和它所对的角,再有另外一个条件,求面积或周长的值”,这类问题通法思路是:全部转化为角的关系,建立函数关系式,如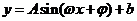 ,从而求出范围,或利用余弦定理以及基本不等式求范围;求具体的值直接利用余弦定理和给定条件即可.
,从而求出范围,或利用余弦定理以及基本不等式求范围;求具体的值直接利用余弦定理和给定条件即可.
18.(12分)
如图,在四棱锥P-ABCD中,AB//CD,且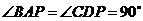 .
.
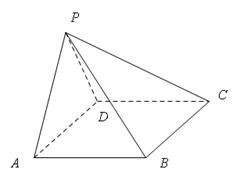
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,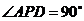 ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.


则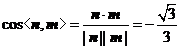 ,
,
所以二面角 的余弦值为
的余弦值为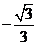 .
.
[考点]面面垂直的证明,二面角平面角的求解
[名师点睛]高考对空间向量与立体几何的考查主要体现在以下几个方面:①求异面直线所成的角,关键是转化为两直线的方向向量的夹角;②求直线与平面所成的角,关键是转化直线的方向向量和平面的法向量的夹角;③求二面角,关键是转化为两平面的法向量的夹角.建立空间直角坐标系和表示出所需点的坐标是解题的关键.
19.(12分)
为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布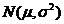 .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在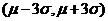 之外的零件数,求
之外的零件数,求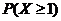 及
及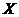 的数学期望;
的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在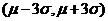 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
|
9.95 |
10.12 |
9.96 |
9.96 |
10.01 |
9.92 |
9.98 |
10.04 |
|
10.26 |
9.91 |
10.13 |
10.02 |
9.22 |
10.04 |
10.05 |
9.95 |
经计算得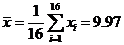 ,
,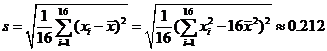 ,其中
,其中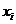 为抽取的第
为抽取的第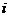 个零件的尺寸,
个零件的尺寸,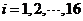 .
.
用样本平均数 作为
作为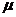 的估计值
的估计值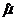 ,用样本标准差
,用样本标准差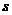 作为
作为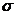 的估计值
的估计值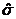 ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计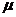 和
和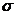 (精确到0.01).
(精确到0.01).
附:若随机变量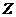 服从正态分布
服从正态分布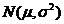 ,则
,则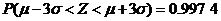 ,
,
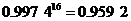 ,
,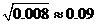 .
.
 试题解析:(1)抽取的一个零件的尺寸在
试题解析:(1)抽取的一个零件的尺寸在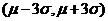 之内的概率为0.9974,从而零件的尺寸在
之内的概率为0.9974,从而零件的尺寸在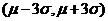 之外的概率为0.0026,故
之外的概率为0.0026,故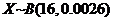 .因此
.因此
 .
.
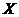 的数学期望为
的数学期望为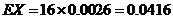 .
.

20.(12分)
已知椭圆C: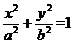 (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1,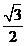 ),P4(1,
),P4(1,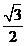 )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
 (2)设直线P2A与直线P2B的斜率分别为k1,k2,
(2)设直线P2A与直线P2B的斜率分别为k1,k2,
如果l与x轴垂直,设l:x=t,由题设知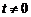 ,且
,且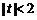 ,可得A,B的坐标分别为(t,
,可得A,B的坐标分别为(t,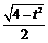 ),(t,
),(t,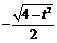 ).
).
则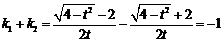 ,得
,得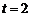 ,不符合题设.
,不符合题设.
从而可设l: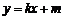 (
(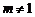 ).将
).将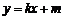 代入
代入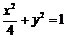 得
得
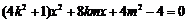
由题设可知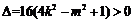 .
.
设A(x1,y1),B(x2,y2),则x1+x2=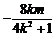 ,x1x2=
,x1x2=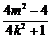 .
.
而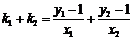
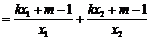
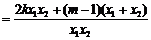 .
.
由题设 ,故
,故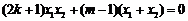 .
.
即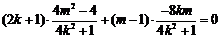 .
.
解得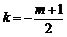 .
.
当且仅当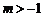 时,
时,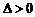 ,欲使l:
,欲使l: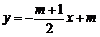 ,即
,即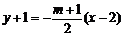 ,
,
所以l过定点(2,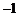 )
)
[考点]椭圆的标准方程,直线与圆锥曲线的位置关系.
[名师点睛]椭圆的对称性是椭圆的一个重要性质,判断点是否在椭圆上,可以通过这一方法进行判断;证明直线过定点的关键是设出直线方程,通过一定关系转化,找出两个参数之间的关系式,从而可以判断过定点情况.另外,在设直线方程之前,若题设中为告知,则一定要讨论直线斜率不存在和存在情况,接着通法是联立方程组,求判别式、韦达定理,根据题设关系进行化简.
21.(12分)
已知函数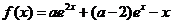 .
.
(1)讨论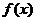 的单调性;
的单调性;
(2)若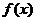 有两个零点,求a的取值范围.
有两个零点,求a的取值范围.

 (二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.[选修4―4:坐标系与参数方程](10分)
在直角坐标系xOy中,曲线C的参数方程为 (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为
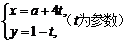 .
.
(1)若a=−1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为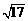 ,求a.
,求a.
[解析]试题分析:(1)先将曲线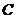 和直线l化成普通方程,然后联立求出交点坐标;(2)直线
和直线l化成普通方程,然后联立求出交点坐标;(2)直线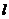 的普通方程为
的普通方程为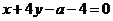 ,设
,设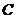 上的点
上的点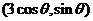 ,
,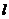 的距离为
的距离为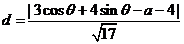 .对a进行讨
.对a进行讨 23.[选修4-5:不等式选讲](10分)
23.[选修4-5:不等式选讲](10分)
已知函数f(x)=–x2+ax+4,g(x)=│x+1│+│x–1│.
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[–1,1],求a的取值范围.
[解析]
试题分析:(1)将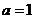 代入,不等式
代入,不等式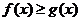 等价于
等价于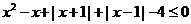 ,对
,对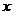 按
按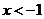 ,
,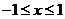 ,
,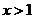 讨论,得出最值的解集;(2)当
讨论,得出最值的解集;(2)当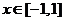 时,
时, .若
.若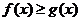 的解集包含
的解集包含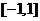 ,
,