1.下列方程中，是关于x的一元二次方程的为(　　 )

A.ax²+bx+c=0　　　　　 B.x²+2x=x²-1　　　 C.3(x+1)²=2(x+1)　　 D.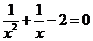　

2.用配方法解下列方程时，配方错误的是(　　 )

A.x²+2x-99=0化为(x+1)²=100　　　　　　　　 B.2x²-7x-4=0化为(x-)²=　

C.x²+8x+9=0化为(x+4)²=25　　　　　 　　　　D.3x²-4x-2=0化为(x-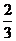)²=　

3.下列函数是二次函数的是( )

A.y=2x+1　　　　 B.y=-2x+1　　　 C.y=x²+2　　　　 D.y=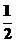x-2

4. 二次函数y=3x²-2x-4的二次项系数与常数项的和是( )

A.1　　　　　　 B.-1　　　　　　　　 C.7　　　　　　 D.-6

5. 以-3和2为根的一元二次方程是(　　 )

　　　 A.x²-x-6=0　　　　 B.x²+x-6=0　　　　 C.x²-x+6=0　　　 D.x²+x+6=0

6. 抛物线向左平移3个单位所得抛物线是(　　 )

A. 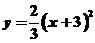　　　　　　　　　　　B.

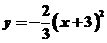C. 　　　　　　　　　　D.

7.关于x的一元二次方程x²+nx+m=0的两根中只有一个等于0，则下列条件正确的是(　　 )

A.m=0，n=0　　　　 B.m≠0，n≠0　　　 C.m≠0，n=0　　　 D.m=0，n≠0

8.要得到抛物线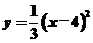，可将抛物线　(　　 )

A．向上平移4个单位　　　　 B．向下平移4个单位

C．向右平移4个单位　　　　 D．向左平移4个单位

9.对于任意实数h，抛物线y=(x-h)²与抛物线y=x²(　　 )

A.开口方向相同　　　 B.对称轴相同　　　　 C.顶点相同　　　 D.都有最高点

10.(广东中考)关于x的一元二次方程x²-3x+m=0有两个不相等的实数根，则实数m的取值　　 范围为(　　 )

　 A.m＞　　　 B.m＜　　　 C.m=　　　　 D.m＜-

11.关于x的一元二次方程(m-2)x²+(2m-1)x+m²-4=0的一个根是0，则m的值是(　 )　 　　　　　　　　　　　　　　　　　　　　　　　　

　　　 　A.2　　　　 B.-2　　　 C.2或-2　　　 D.

12.已知a、b实数且满足(a²+b²)²-(a²+b²)-6=0，则a²+b²的值为　　 (　 　　)

　　 A.3　　 B.-2　　　 3.3或-2　　　 D.-3或2

1.方程3(x+1) ²=2x ²-5 化为一般形式得___________，一次项系数是___，

　不解方程，判别该方程根的情况是___________.

2.从地面竖直向上抛出一小球，小球的高度h(单位：米)与小球运动时间t(单位：秒)的函数关系式是h=9.8t-4.9t.若小球的高度为4.9米，则小球的运动时间为

3.将抛物线y=3x²向左平移2个单位，再向下平移1个单位，所得抛物线为4.若抛物线的顶点为(3,5) ，则此抛物线的解析式可设为

5.若，则=　　　　 .

6.已知的值是10，则代数式的值是　　　　 .

7.二次函数的图象如右图，则一元二次方程的解为.

8.抛物线的顶点是(2，4)，则b＝　 c＝.

9.如果抛物线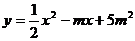与x轴有一个交点，则m=_______________.

　 　10.物线y=x² 向　 平移个 单位,再向平移 个单位,

　就可得y=x²－4x－4.

1.(20分)用适当的方法求解：

　(1)(x+6)²-9=0；　　　　　　　　　　　 (2)；　　　　　　　　　

(3)；　　　　　　　　　　

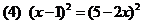
2．(6分)已知一元二次方程kx²+(2k-1)x+k+2=0有两个不相等的实数根，求k的取值范围。

3. (8分)如果一个二次函数的图象经过(-2,0)，(4,0)，(0,4)三点，请求出这个二次函数解析式.

4. (8分)对于函数，请回答下列问题：

(1)图象的对称轴，顶点坐标各是什么？

　　 当x取何值时，函数有最大(小)值，函数最大(小)值是多少？　　　　　　　　　　　　　　　　　　　　　

(2)求抛物线与x轴的交点，与y轴的交点坐标是什么？　　　　　　　　　　　　　　　　　　　　

5. (12分)如图3，是某河上一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的和距离都是1m, 拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯，建立适当坐标系.

(1)求抛物线的解析式.

(2)求两盏景观丁之间的水平距离.