
1、-6的相反数是 。
2、计算: 。
。
3、函数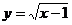 中,自变量x的取值范围是 。
中,自变量x的取值范围是 。
4、一组数据2、3、6、6、8的众数是 。
5、当k 时,方程 没有实数根。
没有实数根。
6、点P(2,3)关于x轴对称的点的坐标是 。
7、已知线段a=2cm,b=3cm,c=6cm,d是a、b、c的第四比例项,那么d= 。
8、梯形的中位线长为6cm,上底长为4cm,那么这个梯形的下底长为 。
二选择题(3×5=15分)
9、下列二次根式中与 是同类二次根式的是( )
是同类二次根式的是( )
A、 B、
B、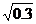 C、
C、 D、
D、
10、下列命题中真命题是( )
A、两个直角三角形是相似三角形 B、两个等边三角形是相似三角形
C、两个等腰三角形是相似三角形 D、相似三角形面积的比等于它所对应的边的比
11、矩形具有而菱形不一定具有的性质是( )
A、对角线互相平分 B、对角线互相垂直
C、对角线相等 D、对边相等
12、 满足b<0,c<0的二次函数
满足b<0,c<0的二次函数 的大致图象是(
)
的大致图象是(
)



13、某化肥厂一月份生产化肥500吨,从二月份起,由于改进操作技术,使得第一季度共生产化肥1750吨,问二、三月份平均每月的增长率是多少?在这个问题中,若二、三月份平均每月的增长率为x,则可得方程( )
A、500(1+x)2=1750 B、500+500(1+x) 2=1750
C、500(1+x)+500(1+x) 2=1750 D、500+500(1+x)+500(1+x) 2=1750
14、计算: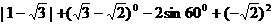
15、化简:a2-(a-2b)(a+b)
16、解不等式 ,并把解集在数轴上表示出来。
,并把解集在数轴上表示出来。
17、已知:x+y=3,x-y=1,求(x2+y2) 2-4x2y2的值。
18、计算: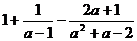
19、已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB有平分线。
求证:AB=DC

20、甲、乙两个蓄水池,蓄满水后的水量都为120立方米,已知甲池有水48立方米,乙池蓄满了水,现甲池开始进水,每小时进水8立方米,同时乙池放水,每小时放水10立方米。
(1)分别写出甲池内的水量,y甲(立方米)与进水时间(t)之间的函数关系式,乙池中的水量y乙(立方米)与放水时间(t)时之间的函数关系及t的取值范围。
(2)经过几小时后,两个池内的水一样多?
21、如图,一飞机于空中A处探测到地面目标C,此时飞行高度AC=1300米,从飞机上看地平面控制点B的俯角α=17°,求飞机A到控制点B的距离?(精确到0.1米,参考数据:
sin17°=0.29,cos17°=0.96,tg17°=0.31,ctg17°=3.3)

22、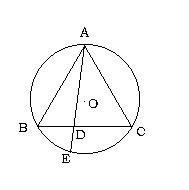 已知:如图,圆内接△ABC中,AB=AC,D是BC边上一点,E是直线AD和△ABC外接圆的交点,求证:AB2=AD.AE
已知:如图,圆内接△ABC中,AB=AC,D是BC边上一点,E是直线AD和△ABC外接圆的交点,求证:AB2=AD.AE
23、已知:如图,以△ABC的边AC为直径的半圆分别交AB、BC于点E、D,△BED与△ABC的面积比为1∶9,ED=2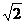 ,O′是△ABC的外接圆圆心。
,O′是△ABC的外接圆圆心。
(1) 求cosB的值;(2)求AC的长;(3)求外接⊙O′的面积。
B卷(50分)
 已知:如图,在正方形ABCD中,F是CD边上的中点,点P在BC上,∠1=∠2,PE⊥BC交AC于点E,垂足为P。求证:AP=3PE。
已知:如图,在正方形ABCD中,F是CD边上的中点,点P在BC上,∠1=∠2,PE⊥BC交AC于点E,垂足为P。求证:AP=3PE。
某农场300名职工耕种51公顷土地,分别种植水稻、蔬菜和棉花,种植这些农作物每公顷所需的职工人数及这些农作物每公顷的预计产值如下表所示:
|
农作物 |
每公顷所需人数 |
每公顷预计产值 |
|
水稻 |
4 |
4.5万元 |
|
蔬菜 |
8 |
9万元 |
|
棉花 |
5 |
7.5万元 |
设水稻、蔬菜、棉花的种植面积分别为x公顷、y公顷、z公顷
(1)用含x的代数式分别表示y和z;
(2)若这些农作物的总产值p满足关系360≤p≤370(x、y、z均为整数),求这个农场应怎样安排水稻、蔬菜、棉花的种植面积才能取得最优效益?
已知:如图,⊙O1与⊙O2外切于点P,AB是两圆外公切线,A、B为切点,AB与O1O2的延长线相交于点C,延长AP交⊙O2于点D,点E在AD的延长线上。
(1) 证△ABP是直角三角形;
(2)若AB.AC=AP.AE,试判断AC与EC是否垂直,并说明理由;
(3)求证:PC=EC;
(4)若AP=4,PD=9/4,求BC/EC的值。
