
1. 若集合 , 则满足
, 则满足 的集合
的集合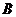 的个数是
的个数是
(A) 6 (B) 7 (C) 8 (D) 10
2. 函数 R 是
R 是
(A) 最小正周期为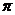 的偶函数
(B) 最小正周期为
的偶函数
(B) 最小正周期为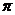 的奇函数
的奇函数
(C) 最小正周期为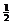
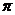 的偶函数 (D) 最小正周期为
的偶函数 (D) 最小正周期为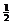
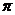 的奇函数
的奇函数
3. 椭圆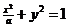 的准线与
的准线与 轴平行, 那么
轴平行, 那么 的取值范围为
的取值范围为
(A)  (B)
(B)
 (C)
(C)
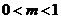 (D)
(D) 
4. 已知| a | =
| b | = 2, a.b = -2, 且(a + b)⊥(a + 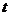 b), 则实数
b), 则实数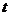 的值为
的值为
(A) –1 (B) 1 (C) –2 (D) 2
5. 光线沿直线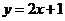 射到直线
射到直线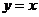 上, 被
上, 被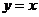 反射后的光线所在的直线方程为
反射后的光线所在的直线方程为
(A) 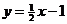 (B)
(B)
 (C)
(C)  (D)
(D) 
6. 若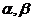 是两个相交平面, 点
是两个相交平面, 点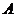 不在
不在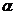 内, 也不在
内, 也不在 内, 则过点
内, 则过点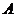 且与
且与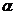 和
和 都平行的直线
都平行的直线
(A) 只有1条 (B) 只有2条 (C) 只有4条 (D) 有无数条
7. 停车场可把12辆车停放在一排上, 当有8辆车已停放后, 而恰有4个空位在一起, 这样的事件发生的概率是
(A)  (B)
(B)
 (C)
(C)
 (D)
(D)

8. 对于二项式
 , 有四个判断: ① 存在
, 有四个判断: ① 存在 , 展开式中有常数项; ② 对任意
, 展开式中有常数项; ② 对任意 , 展开式中没有常数项; ③ 对任意
, 展开式中没有常数项; ③ 对任意 , 展开式中没有
, 展开式中没有 的一次项; ④
存在
的一次项; ④
存在 , 展开式中有
, 展开式中有 的一次项. 上述判断中正确的是
的一次项. 上述判断中正确的是
(A) ①与③ (B) ②与③ (C) ②与④ (D) ①与④
 (第9题) |
9. 给出平面区域 , 如图所示, 其中
, 如图所示, 其中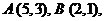
 . 若使目标函数
. 若使目标函数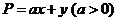 取得最大值
取得最大值
的最优解有无穷多个, 则 的值为
的值为
(A) 4 (B)
2 (C) 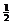 (D)
(D)
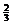
10. 已知函数 , 函数
, 函数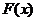 定义如下: 当
定义如下: 当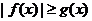 时,
时, 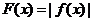 ; 当
; 当 时,
时,  .
.
那么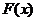
(A) 有最小值0, 无最大值 (B) 有最小值-1, 无最大值
(C) 有最大值1, 无最小值 (D) 无最小值, 也无最大值
11. 请举出一个反例: ______, 说明命题“奇函数必存在反函数”是假命题.
12. 圆心在直线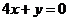 上, 且过点
上, 且过点 的圆的方程是 _______ .
的圆的方程是 _______ .
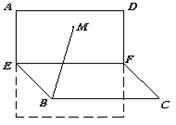 (第13题) |
13. 正方形 的边长是2,
的边长是2,
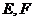 分别是
分别是
和 的中点, 将正方形沿
的中点, 将正方形沿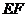 折成直二面角(如
折成直二面角(如
图所示). 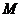 为矩形
为矩形 内一点,
如果
内一点,
如果
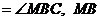 和平面
和平面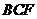 所成角的正切值为
所成角的正切值为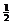 ,
,
那么点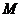 到直线
到直线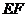 的距离为
_______ .
的距离为
_______ .
14. 某健康中心研究认为:身高为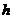 (cm)的人的其理想体重
(cm)的人的其理想体重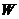 (kg),应符合公式
(kg),应符合公式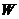 =22
=22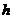 2 (kg),且定义体重在理想体重±10%的范围内,称为标准体重;超过10%但不超过20%者,称为微胖;超过20%者,称为肥胖, 微胖及肥胖都是过重的现象. 对身高
2 (kg),且定义体重在理想体重±10%的范围内,称为标准体重;超过10%但不超过20%者,称为微胖;超过20%者,称为肥胖, 微胖及肥胖都是过重的现象. 对身高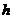 ,体重
,体重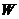 的人,体重过重的充要条件为
的人,体重过重的充要条件为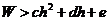 ,则
,则 __________ .
__________ .
15. (本小题满分14分)

16. (本小题满分14分)
已知数列{ }是首项为
}是首项为 等于1且公比
等于1且公比 不等于1的等比数列,
不等于1的等比数列, 是其前
是其前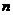 项的和,
项的和, 成等差数列.
成等差数列.
(1) 求和  ;
;
(2) 证明 12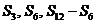 成等比数列.
成等比数列.
17.(本小题满分14分)
设甲、已、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5.
(1) 三人各向目标射击一次,求至少有一人命中目标的概率;
(2) 三人各向目标射击一次,求恰有两人命中目标的概率;
(3)若甲单独向目标射击三次,求他恰好命中两次的概率.
18. (本小题满分14分)
 (第18题) |
如图, 在四棱锥 中,顶点
中,顶点 在底面
在底面 上的射影恰好落在
上的射影恰好落在 的中点
的中点 上,又∠
上,又∠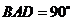 ,
, ,且
,且
=1:2:2.
(1) 求证: 
(2) 若 , 求直线
, 求直线 与
与 所成的角的余弦值;
所成的角的余弦值;
(3) 若平面 与平面
与平面 所成的角为
所成的角为 , 求
, 求 的值.
的值.
19. (本小题满分14分)
已知奇函数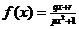 有最大值
有最大值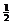 , 且
, 且 , 其中实数
, 其中实数 是正整数.
是正整数.
(1) 求 的解析式;
的解析式;
(2) 令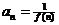 , 证明
, 证明 (
(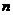 是正整数).
是正整数).
20. (本小题满分14分)
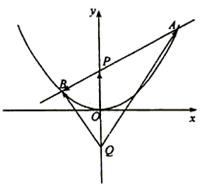 (第20题) |
如图,过抛物线 的对称轴上任一点
的对称轴上任一点 作直线与抛物线交于
作直线与抛物线交于 两点,点
两点,点 是点
是点 关于原点的对称点.
关于原点的对称点.
(1) 设点 分有向线段
分有向线段 所成的比为
所成的比为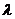 ,证明:
,证明:
 ;
;
(2) 设直线 的方程是
的方程是 ,过
,过 两点的圆
两点的圆 与抛物线在点
与抛物线在点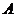 处有共同的切线,求圆
处有共同的切线,求圆 的方程.
的方程.
2006年杭州市第二次高考科目教学质量检测
数学参考评分标准(文科)
11. 如 或
或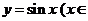 R)等.
12.
R)等.
12.  .
.
13.  .
14. (24.2,0,0 )
.
14. (24.2,0,0 )
15. (本小题满分14分)
(1) 由 --- 5分
--- 5分
(2) 
16. (本小题满分14分)
由 成等差数列, 得
成等差数列, 得 ,即
,即
 --- 2分
--- 2分
变形得  所以
所以 (舍去). --- 4分
(舍去). --- 4分
(1) 
 ;
;
--- 4分
(2) 由 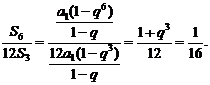
 ,
,
所以12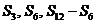 成等比数列.
--- 4分
成等比数列.
--- 4分
17.(本小题满分14分)
设 表示“第
表示“第 人命中目标”,
人命中目标”, =1,2,3.
=1,2,3.
这里, 相互独立,且
相互独立,且 =0.7,
=0.7,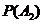 =0.6,
=0.6, =0.5. --- 2分
=0.5. --- 2分
(1) 至少有一人命中目标的概率为
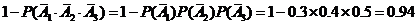 ;
--- 4分
;
--- 4分
(2) 恰有两人命中目标的概率为
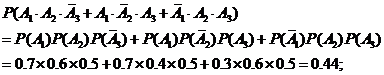 --- 4分
--- 4分
(3) 所求概率为 --- 4分
--- 4分

18. (本小题满分14分)
因为 中点
中点 为点
为点 在平面ABCD内的射影, 所以
在平面ABCD内的射影, 所以 底面
底面 . 以
. 以 为坐标原点,
为坐标原点,  所在直线为
所在直线为 轴,
轴,  所在直线为
所在直线为 轴, 建立空间直角坐标系
轴, 建立空间直角坐标系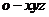 (如图).
(如图).
(1)设 , OP = h则依题意得:
, OP = h则依题意得:

|
--- 4分 |
 .
.
∴ =
=  ,
,
 =
=  ,
,
于是 .
. =
=  ,
∴
,
∴
(2)由 , 得h = a, 于是
, 得h = a, 于是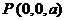 ,
,
|
--- 5分 |
∵ =
=  ,
,
 =
= 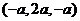 ,
∴
,
∴ .
. =
=
 ,
,
cos< ,
, > =
> =  =
=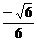 , ∴ 直线
, ∴ 直线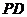 与
与 所成的角的余弦值为
所成的角的余弦值为 ;
;
(3) 设平面 的法向量为m, 可得m = (0,1,0 ),
的法向量为m, 可得m = (0,1,0 ),
设平面 的法向量为n =
的法向量为n =  , 由
, 由 =
=
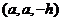 ,
,  =
=
 ,
,
∴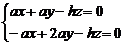 ,
解得n = (1, 2 ,
,
解得n = (1, 2 , ), ∴ m•n = 2 ,
), ∴ m•n = 2 ,
cos< m, n > = 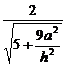 , ∵ 二面角为
, ∵ 二面角为 , ∴
, ∴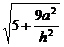 =
4,
=
4,
解得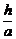 =
= ,即
,即 =
= .
--- 5分
.
--- 5分
(以传统方法解答相应给分)
19.(本小题满分14分)
(1) 由奇函数 可得
可得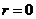 ,
--- 2分
,
--- 2分
x > 0时,由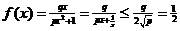 ① 以及
① 以及 ②
--- 4分
②
--- 4分
可得到 ,
, 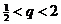 , 只有
, 只有 , ∴
, ∴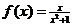 ; --- 2分
; --- 2分
(2)  ,
--- 2分
,
--- 2分
则由 (
(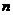 是正整数),
是正整数),
可得所求证结论. --- 4分
20. (本小题满分14分)
(1) 依题意,可设直线 的方程为
的方程为  代入抛物线方程
代入抛物线方程 得
得
 ①
①
设 两点的坐标分别是
两点的坐标分别是
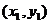 、
、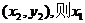 、
、 是方程①的两根.
是方程①的两根.
所以  ---
2分
---
2分
由点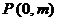 分有向线段
分有向线段 所成的比为
所成的比为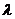 ,得
,得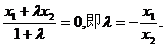
又点 与点
与点 关于原点对称,故点
关于原点对称,故点 的坐标是
的坐标是 ,从而
,从而 .--- 2分
.--- 2分
 ---
2分
---
2分


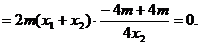 所以
所以 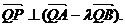 ---
2分
---
2分
(2) 由 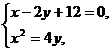 得点
得点 的坐标分别是(6,9)、(-4,4), --- 2分
的坐标分别是(6,9)、(-4,4), --- 2分
由  得
得

所以抛物线  在点
在点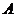 处切线的斜率为
处切线的斜率为 ,
--- 2分
,
--- 2分
设圆 的圆心为
的圆心为 , 方程是
, 方程是
则 解得
解得

则圆 的方程是
的方程是  (或
(或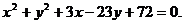 )
)
--- 2分